이 포스트는 개인적으로 공부한 내용을 정리하고 필요한 분들에게 지식을 공유하기 위해 작성되었습니다. 지적하실 내용이 있다면, 언제든 댓글 또는 메일로 알려주시기를 바랍니다.
00. 들어가며
2020년, Facebook에서 Wav2Vec 2.0을 발표했다. 앞서 살펴보았던 Wav2Vec 및 VQ-Wav2Vec과 마찬가지로, Wav2Vec 2.0 역시 음성 신호가 전사되어있는 labeled data가 부족하다는 이슈에 대해 self-supervised learning 기법으로 pre-training 하는 방법론을 제시한다. pre-training이 완료된 Wav2Vec 2.0은 이후 Connectionist Temporal Classification(CTC) loss를 활용해서 적은 양의 labeld data로 fine-tuning 하여 활용할 수 있다.
놀라운 것은 Wav2Vec 2.0으로 pre-training된 모델이 단지 10분 분량의 labeled data만으로 fine-tuning 되었을 때 Librispeech 데이터셋 기준으로 Word Error Rate(WER)이 깨끗한 음성에 대해서는 4.8을, 이외의 음성에 대해서는 8.2를 기록했다는 점이다. 즉, 매우 적은 양의 데이터만 있으면 어느 정도 동작하는 음성 인식기를 쉽게 만들 수 있게 되었다는 점에서 큰 의의가 있는 것이다.
[그림01] 학습 시간에 따른 Wav2Vec2.0의 성능
한편, TIMIT phoneme recognition 문제 등에서 SOTA를 달성했으며, labeled data를 더욱 줄여서 오로지 1시간의 labeled data만으로 fine-tuning 했음에도 100배 많은 labeled data로 학습한 기존의 SOTA self-training 방식 모델보다 더욱 나은 성능을 보였다. 게다가 960 시간의 모든 Libreespeech의 labeled data를 활용했을 때는 깨끗한 음성의 경우 WER이 1.8, 그 이외에 대해서는 3.3을 달성하였다.
세상에는 다양한 방언 뿐만 아니라 7,000 여 개나 되는 언어가 존재한다. Wav2Vec 2.0은 이렇게 다양한 언어에 대해서도 매우 적은 양의 데이터만 있으면 높은 정확도를 보이는 음성 인식 모델을 구축할 수 있는 세상을 열었다. 그렇다면, 과연 어떻게 작동하는지 Wav2Vec 2.0을 살펴보겠다.
01. 모델
[그림02] pre-training 과정에서의 Wav2Vec 2.0 모델 아키텍처
[그림02]은 pre-training 과정에서의 Wav2Vec 2.0 모델 아키텍처를 보여준다.
Feature Encoder
기존 Wav2Vec 모델들과 마찬가지로 feature encoder 네트워크 $f:\mathcal{X} \mapsto \mathcal{Z}$가 존재한다. multi-layer CNN으로 구성된 이 네트워크는 원시 음성 신호 sequence 입력값인 $\mathcal{X}$를 입력 받아서 매 $T$ 시점마다 latent speech representation인 $\mathbf{z}_1, … , \mathbf{z}_T$를 출력한다. 이후 latent speech representation $\mathbf{z}_1$, … , $\mathbf{z}_T$는 두 모듈에 각각 나뉘어서 입력값으로 흘러간다.
Contexualized Representations with Transformers
latent speech representation이 입력되는 한 모듈은 contextulized representation을 위한 transformer 모듈 $g:\mathcal{Z} \mapsto \mathcal{C}$이다. 즉, $\mathbf{z}_1, … , \mathbf{z}_T$ sequence가 입력되면, transformer 블록(transformer encoder 블록)에 의해 sequence 내 모든 맥락 정보가 파악된 $\mathbf{c}_1, … , \mathbf{c}_T$ sequence가 출력된다.
특징으로는, transformer 블록에서는 기본적인 absolute positional embedding을 사용하지 않고, convolution 연산을 통해서 relative positional embedding과 유사한 효과를 주었다고 한다.
Quantization Module
[그림03] G개의 codebook, V개의 code words를 활용한 Wav2Vec 2.0의 quantization 모듈
latent speech representation $\mathbf{z}$가 입력되는 또 다른 모듈은 quantization 모듈 $\mathcal{Z} \mapsto \mathcal{Q}$ 이다. vector quantization의 개념이 헷갈리면 [여기]를 참고하면 좋을 것이다. [그림03]의 중앙을 보면 codebook 행렬 $e \in \mathbb{R}^{V \times d / G}$이 $G$개 존재하여 $G \times V$ 크기의 multiple codebooks를 이루고 있다. 즉, 하나의 codebook은 [그림03] 중앙에서 보여지는 $V$개의 code word 벡터(작은 네모 한 개) sequence 한 행에 대응된다. 이들은 모두 학습 가능한 파라미터로 구현된다. 즉, codebook을 embedding matrix로, code word를 embedding 벡터로 생각하자. (참고로 저자는 $G=2$, $V=320$을 사용했다.)
이러한 세팅 하에서 quantization 모듈에서 일어나는 일들을 설명해보겠다. encoding 된 $z_t$가 주어졌을 때, $z_t$는 레이어를 통과하여 logit으로 변환되고, gumbel softmax(참고) 및 argmax를 통해 one-hot encoding 된 후(즉, 이산화 과정), 마치 NLP에서 embedding matrix에서 특정 단어에 해당하는 embedding 벡터를 뽑아내듯, 각 codebook 내에서 하나의 code word 벡터를 골라낸다. code word 벡터는 $G$개의 codebook 행렬에서 각각 하나씩 추출됨에 따라 총 $G$개의 $e_{1}, …, e_{G} \in \mathbb{R}^{d / G}$ 벡터들로 추출될 것이다. 이후, $G$개의 벡터 모두를 concatenate 하여 $e_{t} \in \mathbb{R}^{d}$를 만든다([그림03]에서의 세번째 과정). 여기서 linear transformation $\mathbb{R}^{d} \mapsto \mathbb{R}^{f}$을 통해서 quantized representation $q_{t} \in \mathbb{R}^{f}$를 최종적으로 만들어낸다.([그림03]에서의 마지막 과정)
codebook과 code word의 의미
복잡하다. 그런데 도대체 codebook과 code word가 의미는 것은 무엇일까? code word는 일종의 음소(phoneme)에 대한 representation이라고 생각하면 될 것 같다. 아무리 언어가 다르더라도 사람이 발음할 수 있는 음소는 사실상 유한하다고 봐도 좋기 때문에, 이를 마치 embedding 벡터로 표현한 것이 code word인 셈이다. 또한 이들이 모여 만들어진 행렬이 codebook인 셈이다. 즉, $V$개의 음소 중 현 시점에 음성 encoding 벡터 $z_t$와 가장 대응될 음소 벡터를 이산화 과정을 통해 골라낸 것이 $q_t$라고 할 수 있다.
수식으로 표현한 gumbel softmax
원 논문에 나와 있는 수식으로 다시 살펴보겠다. encoder를 거쳐 나온 $\mathbf{z}$는 레이어를 통과하여 로짓으로 $\mathbf{l} \in \mathbb{R}^{G \times V}$ 변환된다. 이때 $G$개의 multiple codebook을 사용하므로, $g$번째 codebook에서 $v$번째 code word 벡터가 선택될 확률을 gumbel softmax로 표현하면 다음과 같다.
$p_{g, v} = \cfrac{\exp(l_{g, v} + n_v) / \tau }{\sum_{k=1}^{V} \exp (l_{g, k} + n_k) / \tau}$
이때 $\tau$는 gumbel softmax의 non-negative temperature, $n=- \log ( \log (u) )$이며, $u$는 uniform distribution $\mathcal{U}(0, 1)$에서 랜덤하게 sampling된 값이다. gumbel softmax의 특징답게, forward pass에서는 확률 값에 대한 argmax를 통해 나온 index에 해당하는 codeword가 선택되지만, backward pass에서는 gumbel softmax에 대한 기울기가 계산되어 학습된다.
02. 학습 방식
Wav2Vec 2.0은 pre-training 과정에서 BERT와 유사하게 마스킹 기법을 도입한 것이 특징이다. 학습의 목적식은 마스킹된 부분에 해당되는 quantized representation인지, 다른 부분에 해당되는 quantized representation인지를 구분하는 문제로 구성되어 있다. pre-training을 마치면, labeled data로 fine-tuning이 진행된다.
마스킹
마스킹 기법을 살펴보겠다. 마스킹은 feature encoder의 출력값인 $\mathbf{z}$를 transformer block인 context network에 입력하기 전에 수행된다. transformer block의 self-attention 효과를 보기 위해 마스킹을 적용하는 것이므로, 당연히 quantization 모듈의 입력값에는 마스킹을 수행하지 않는다.
그 과정은 다음과 같다.
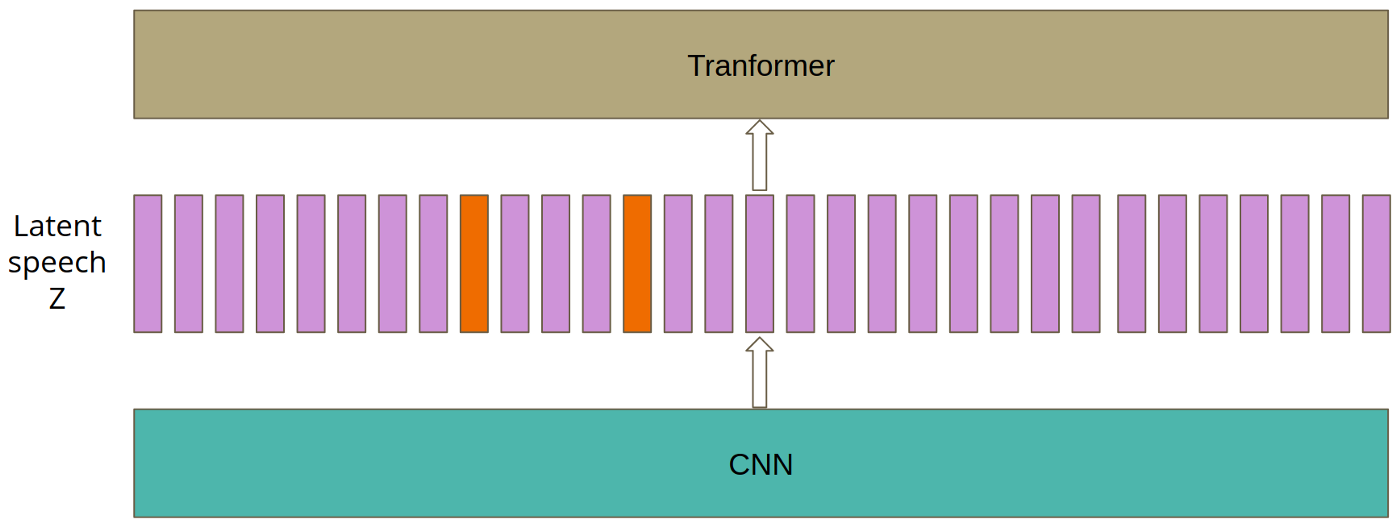[그림04] masking 인덱스의 시작점을 선택함
[그림05] masking을 진행함
우선, [그림04]와 같이 $p=0.065$의 확률로 $\mathbf{z}$ sequence를 마스킹의 시작점으로 선정한다. 그리고는 [그림05]와 같이 $M=10$ 만큼 연달아 마스킹을 수행한다. 이때, $p$와 $M$은 하이퍼파라미터이다. 시작 지점에 따라서 당연히 마스킹이 겹치는 경우가 생길 수 있다. 마스킹은 trained feature vector로 마스킹되는 부위를 대체하는 방식이며, 모든 마스킹 부위는 동일하게 해당 feature vector를 사용한다.
목적식(Loss Function)
$\mathcal{L} = \mathcal{L}_{m} + \alpha \mathcal{L}_d$
loss function은 위와 같이 정의된다. $\mathcal{L}_m$은 다른 Wav2Vec 버전들과 유사하게 pre-training 과정에서 계산되는 contrastive loss term이다. 추가로 $\mathcal{L}_d$ term이 더해져 있는데, 이는 diversity loss라고 부른다. 이때 $\alpha$는 하이퍼파라미터이다.
Contrastive Loss
$\mathcal{L}_m = - \log \cfrac{ \exp{ (sim(\mathbf{c}_t , \mathbf{q}_t)/ \mathcal{κ}) } }{ \sum _ {\tilde{\mathbf{q}} \sim \mathbf{Q}_t} \exp{(sim(\mathbf{c}_t , \tilde{\mathbf{q}})/\mathcal{κ})}}$
contrastive loss term $\mathcal{L}_m$은 위와 같다. 수식을 뜯어보자. [그림02]와 함께 보면 좋을 것이다. $t$는 마스킹이 수행된 time step이다. $\mathbf{c}_t$는 마스킹이 수행된 time step에서 추출된 context representation으로, 해당 시점 기준으로 전체 sequence에 대한 맥락 정보가 반영되어 있다. $\tilde{\mathbf{q}} \in \mathbf{Q}_t$는 $K$개의 distractor(방해 요소)와 정답 역할을 하는 1개의 $\mathbf{q}_t$로 구성되어 총 $K+1$개의 candidate quantized representation이다. 이때, $K$개의 distractor는 동일 발화의 다른 마스크 time step으로부터 랜덤하게 추출한 값들이다. $κ$는 학습 과정에서 temperature 역할을 하는 상수값이며, $sim()$ 함수는 cosine similarity 연산이다.
따라서, 이를 종합해 볼 때, contrastive loss는 마스킹 $t$시점 context representation $\mathbf{c} _ t$이 주어졌을 때 정답에 해당하는 $\mathbf{q} _ t$를 오답 역할을 하는 다른 candidate quantized representation 가운데서 구분해내는 역할을 한다.
Diversity Loss
$\mathcal{L}_d = \cfrac{1}{GV} * (-H(\bar{p} _ g)) = \cfrac{1}{GV} \sum _ {g=1}^G \sum _ {v=1}^V \bar{p} _ {g, v} \log(\bar{p} _ {g,v})$
diversity loss $\mathcal{L}_d$은 위와 같으며, 일종의 regularization 기법이다. 저자가 사용한 codebook의 수 $G=2$개였으며, 각각의 codebook 내에서 $V=320$개의 code word를 사용했다. 즉, 첫번째 codebook에서 320가지의 quantized representation이 나올 수 있고, 두번째에서도 마찬가지이므로, 총 $320 \times 320 = 102400$가지의 quantized representation 조합이 나올 수 있다.
그런데 우리는 Wav2Vec 2.0이 실제로 이 모든 조합의 확률을 다 고려해서 골고루 quantized representation을 만드는지 알 수 없다. 수많은 code word 선택에 대한 경우의 수가 있는데, 제대로 활용하지 못한다면 codebook을 활용할 이유가 없는 것과 다름 없다.
저자는 이러한 이슈를 방지하기 위해서 정보 이론의 엔트로피 개념인 $H(X) = - \sum_{x} P(x) \log{(P(x))}$ 를 도입했다. 정보 엔트로피는 균등한 분포 하에서 가장 큰 값을 가진다. 예를 들어서, 앞뒷면의 확률이 모두 동일하게 1/2인 동전을 던질 때의 엔트로피가 앞뒷면의 확률이 불균등한 동전을 던질 때보다 엔트로피가 높다. 요컨대, 저자는 엔트로피를 극대화하기 위한 term을 diversity loss에 포함하여 모든 Wav2vec 2.0 모델이 모든 code word를 균등하게 고려할 수 있게 설계한 것이다.
Fine-tuning
모델이 pre-training을 마치고 나서, fine-tuning 단계에서는 quantization이 활용되지 않는다. 그대신, 무작위로 초기화된 linear projection layer를 모델의 최상단에 두고, context representation $\mathbf{c}$를 통과시키는 방식이다. 이 레이어는 풀고자 하는 task의 어휘(vocabulary)의 수를 의미하는 $C$개 class만큼의 차원으로 projection 한다. 그 후, CTC loss 및 SpecAugment 기법 등을 이용해서 labeled data에 대해 fine-tuning 된다. 또한 저자는 fine-tuning 단계에서도 마스킹 기법을 그대로 유지했다고 한다.
03. 결론과 느낀 점
정리하자면, Wav2Vec 2.0은 기존 Wav2Vec 버전들과 유사하게 self-supervised learning, 그중에서도 contrastive learning을 이용해서 학습했다. 무엇보다 end-to-end로 transformer 블록을 활용했다는 점은 VQ-Wav2Vec과의 차이점이기도 하다. 그리고 multiple codebook을 효과적으로 이용하기 위해 diversity loss를 사용한 것도 독특하다.
NLP에서의 언어모델도 대규모 학습 데이터로 pre-training을 하지만, 특정 언어에 종속적인 경우가 많다. Wav2Vec 2.0은 언어모델과는 다르게 특정 언어에 종속되지 않고 다양한 언어 및 방언에 확장될 수 있다는 점이 굉장히 인상 깊다. Wav2Vec 2.0을 시작으로 하여 음성 인식 분야의 진입 장벽이 굉장히 낮아져서 추후 모두가 쉽사리 음성 AI 기술을 구현할 날이 곧 올 것만 같다.
04. 참고 문헌
[1] 원 논문 : Baevski, Alexei, et al. “wav2vec 2.0: A framework for self-supervised learning of speech representations.” Advances in Neural Information Processing Systems 33 (2020): 12449-12460.
[2] Łukasz Sus의 블로그 : https://towardsdatascience.com/wav2vec-2-0-a-framework-for-self-supervised-learning-of-speech-representations-7d3728688cae
[3] 정보 엔트로피 : 위키피디아