이 포스트는 개인적으로 공부한 내용을 정리하고 필요한 분들에게 지식을 공유하기 위해 작성되었습니다. 지적하실 내용이 있다면, 언제든 댓글 또는 메일로 알려주시기를 바랍니다.
상당 부분 ratsgo’s speech book 내용을 참고하였습니다. ratsgo 님께 감사드립니다.
01. 개요
Recurrent Neural Network(RNN) 또는 Transformer 등은 sequence 데이터를 효과적으로 학습할 수 있는 모델로, 음향 신호 정보를 입력 받아서 음소(단어나 subword라고도 할 수 있겠으나, 여기서는 음소라 하겠다.)의 sequence를 예측하는 task 등에 활용될 수 있다.
그런데 현실적으로는 단순히 sequence를 학습하는 모델을 활용한다고 해도 이러한 sequence labelling task를 쉽게 해결하지는 못한다. 왜냐하면, 음향 신호 데이터와 같은 sequence 데이터들은 보통 입력 데이터들이 학습하기 좋게 잘 쪼개져 있지 않다(un-segemented). 즉, 입력 정보와 레이블 간에 명시적인 정렬 관계(alignment)를 정의하기 어렵다. (이는 손글씨 인식이나 제스처 인식 문제도 해당된다.)
예를 들어, “안녕하세요”라는 발화에 대해서, 누군가는 “안~녕~하세요~”라고 할수도 있고, 또 다른 누군가는 “~안녕하~세~요”라고 할수도 있다. 그러면, MFCC와 같은 음향 신호 데이터 구간의 어느 시점부터 어느 시점까지가 “안”으로 레이블링 되어야 하는지, 또 어디까지가 “녕”으로 레이블링 되어야 하는지 일일이 구분하기 어려운 문제가 생긴다.
이러한 이유로, 입력 음향 신호 데이터는 대게 25ms 정도의 단위로 잘개 쪼개어 피처로써 활용하는데, 그렇다고 쪼개진 각 프레임마다 음소 레이블을 달아주는 것 또한 매우 현실적이지 않다. 사람마다 다르게 발음하는 모든 음성 신호 데이터에 사람이 인지하기도 쉽지 않은 25ms 단위로 레이블을 다는 것은 비용과 정확도 모두 비효율적이기 때문이다.
Connectionist Temporal Classification(CTC)는 이러한 문제를 해결하기 위해 독특한 방식을 제안한다. 이는 학습 데이터에 대해서 pre-segmentation 과정을 통해 입력 정보와 레이블 간 명시적인 정렬 관계를 만드는 과정을 거치지 않고도, 곧장 un-segmented sequence에 대해 음소의 sequence를 예측할 수 있는 방식이다. 즉, $p(label | \mathbf{x})$를 바로 예측할 수 있는 것이다!
02. 훑어보는 CTC 알고리즘
입력되는 음향 신호 데이터의 sequence는 $X=[x_1, x_2, …, x_T]$라 하고, 이에 대응하는 출력 음소 sequence를 $Y=[y_1, y_2, …, y_U]$라고 하자. CTC 알고리즘은 $X$가 주어졌을 때, $Y$에 대한 확률을 부여할 수 있다. 과연 어떻게 CTC 알고리즘이 $X$와 $Y$간의 정렬 관계를 파악하여 $P(Y|X)$를 모델링할 수 있을까? 그 방식이 바로 CTC 알고리즘의 핵심이다.
훑어보는 CTC 알고리즘의 입력 벡터
CTC 알고리즘은 일종의 손실(loss)을 구하는 방식이라고 봐도 큰 무리가 없을 것 같다. CTC 알고리즘은 딥러닝 모델(예를 들면 RNN)의 마지막 레이어에서 구현되는데, 시점 $t$마다 출력되는 음소들에 대한 확률 벡터 값들을 CTC 알고리즘의 입력으로 받으며, CTC 알고리즘에 의해 최종적으로 손실(CTC loss)과 기울기를 계산한다.

위 그림은 CTC 레이어가 입력으로 확률 벡터 값들을 받는 과정을 보여준다. 음향 신호 sequence가 주어졌다고 해보자. 이는 RNN(또는 Transformer와 같은 sequence 처리 모델)을 통과하여 각 time step에 따라서 ‘음소 개수 + 1(blank token $\epsilon$)’개 차원의 확률 벡터가 출력될 것이다. 이 확률 벡터가 CTC 레이어의 입력이 되는 것이다. 특별히, 확률 벡터를 구성할 때 음소뿐만 아니라, $\epsilon$ 이라는 blank token을 추가로 사용한다는 것이 특징이다. 예를 들어, 한국어의 전체 음소 수가 42개라면, CTC 레이어는 42개의 한국어 음소에 1개의 blank token $\epsilon$을 더해 총 43개의 음소들로 이루어진 43차원의 확률 벡터를 입력으로 받는다.
훑어보는 blank token과 정렬(alignment)
blank token $\epsilon$은 왜 필요한 것일까? 만약, 음성 신호 sequence $x_1, x_2, x_3, x_4, x_5, x_6, x_7$가 주어졌고, 이에 대응되는 음소 레이블 sequence $y_1, y_2, y_3, y_4, y_5, y_6, y_7$이 각각 h, h, e, l, l, l, o라고 하면, 최종적으로 이들을 decoding 하는 과정의 출력값은 “hello”가 아닌, “helo”가 되어버린다. 왜냐하면, CTC는 decoding 시 반복되는 문자를 merge 하기 때문이다. blank token $\epsilon$은 이러한 현상을 막기 위해 도입된 특별한 token이다.
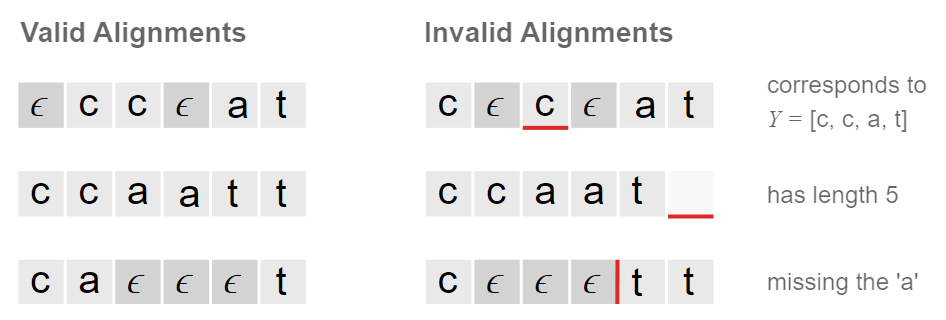
위와 같이, 음소 레이블 sequence $Y$가 단어 cat을 표현하려고 한다고 해보자. CTC 알고리즘은 위의 그림과 같은 방식으로 음소와 blank token $\epsilon$을 적절히 조합하여 음소와 $Y$의 정렬 관계의 다양한 경우들을 표현할 수 있다. 즉, 사람마다 다르게 발음되어 제각각일 수 있는 음향 신호 sequence $X$에 대해서 프레임마다 명시적인 label이 없다고 하더라도 알고리즘 자체적으로 $X$와 $Y$의 정렬 관계를 표현할 수 있는 것이다.
아직 구체적으로 어떻게 손실과 기울기를 구한다는 것인지는 다루지 않았으나, CTC 알고리즘이 손실과 기울기를 구함에 있어서 이와 같은 정렬 관계의 다양한 경우들을 고려할 수 있다는 점을 꼭 짚고 가자!
훑어보는 CTC 알고리즘의 decoding

위 그림은 CTC 알고리즘으로 학습을 마친 모델이 최종적으로 음성 신호 sequence를 decoding 하는 방식을 도식화한 것이다. 우선적으로 반복되는 token을 병합하고, $\epsilon$ blank token을 제거함으로써 최종 출력 sequence를 완성한다.
03. 조금 더 들여다보는 CTC 알고리즘
앞서 “훑어보는 blank token과 정렬(alignment)”에서 살펴보았듯, CTC 알고리즘은 음소와 blank token $\epsilon$의 적절한 조합으로 정렬 관계를 표현한다. 이때 label의 sequence를 $\mathbf{l}$(e.g., h, e, l, l, o)이라고 하고, label 시작과 끝, 그리고 사이사이에 blank token $\epsilon$(-로 표기)을 넣은 sequence를 $\mathbf{l}’$(e.g., -, h, -, e, -, l, -, l, -, o, -)이라고 하겠다.
CTC에서의 정렬 관계는 아래와 같은 3가지 특징이 있다.
self-loop: 현재 token이 반복해서 나올 수 있다. (e.g., “CAT”의 경우, “CCAAT” 가능)left-to-right: 역방향으로 전이되지 않는다. non-blank token을 두 개 이상 건너뛰어 전이되지도 않는다. (e.g., “CAT”의 경우, “TAC”처럼 전이되지 않으며, “CTA”처럼 전이되지도 않음)blank 관련: blank에서 non-blank로, 또는 non-blank에서 blank로 전이될 수 있다.
CTC 알고리즘의 핵심을 결론부터 말하자면, CTC 알고리즘은 label $\mathbf{l}$이 sequence로 주어졌을 때, time step에 따라 sequence $\mathbf{l}’$의 전이 경로가 될 수 있는 각각의 경우들을 그래프로 표현할 수 있고, 이에 대해 Hidden Markov Model에서처럼 forward algorithm 및 backward algorithm을 적용할 수 있다. forward & backward algorithm은 우도($p(label | \mathbf{x})$, 즉 $p(\mathbf{l} | \mathbf{x})$)를 구하는 데 활용되며, 우도에 대해 gradient를 계산하여 backpropagation을 수행함으로써 학습하게 된다.
왜 이렇게 forward & backward algorithm까지 쓰면서 복잡하게 우도를 구해야 하는 것일까? 만약, 음향 신호 sequence의 프레임마다 어떤 음소인지 잘 label이 되어있다면, 단순히 cross entropy loss를 최소화하면 된다. 그러나 계속 말하지만, 음향 신호 데이터는 정답 label의 sequence와 명시적인 정렬 관계를 파악하여 label을 다는 행위가 무척 어렵다. 따라서 forward & backward algorithm을 쓰는 것이다.
Label to Graph

label $\mathbf{l}$이 h, e, l, l, o로 주어졌을 때, $\mathbf{l}’$(-, h, -, e, -, l, -, l, -, o, -)을 세로축으로, 각 time step을 가로축으로 하여, time step에 따른 가능한 $\mathbf{l}’$의 token 간 전이를 그래프로 표현하면 위 그림의 왼쪽과 같다. 여기서 언어 조음 규칙상 절대 발음될 수 없는 경우(예컨대, -, -, -, h, e, l, l, o)의 sequence를 제외하면 위 그림의 오른쪽과 같아진다.(이후 오른쪽 그림만을 대상으로 한다.)
이때 화살표로 표현되는 각 경로들은 CTC의 decoding 과정을 통해서 label $\mathbf{l}$(h, e, l, l, o) sequence를 만들어낼 수 있는 $\mathbf{l}’$ token들의 전이 경로들이다. 예를 들어, 그림을 기준으로 검정색 실선은 -, -, h, e, l, -, l, o의 sequence를 의미하고, 초록색 실선은 h, e, l, -, l, o, -, -의 sequence를 의미한다. 모두 decoding을 한다면 blank token을 제거하고 반복되는 문자를 합침으로써 label $\mathbf{l}$을 만들 수 있다.
$\pi$는 이와 같이 위 그래프에서 좌측 상단으로부터 우측 하단에 이르는 가능한 경로 가운데 하나를 표기한다. 그리고 각각의 동그라미는 개별 확률값을 의미한다. 예컨대, 그림에서 3번째 행, 2번째 열의 동그라미는 $y_3^2$ 로 표기한다. 혹은 $y_-^2$로 표기할 수 있는데, 이는 $t$=2 시점에 -가 나타날 확률을 의미한다. 즉, CTC 알고리즘의 입력값을 만들어내는 RNN + softmax에서 나온 값이다.
CTC 알고리즘에서는 각 상태를 조건부 독립으로 가정한다. 따라서 음향 신호 sequence $\mathbf{x}$가 주어졌을 때, $\pi$가 나타날 확률은 다음과 같이 표현할 수 있다.
$p(\pi | \mathbf{x}) = \prod_{t=1}^{T}y_{\pi_t}^t$
이는 $t$시점에 경로 $\pi$ 상의 token인 $\pi_t$가 나타날 확률값들을 모두 곱한 값으로, 결국 $\pi$가 나타날 확률이다. 한편, $\pi$가 될 수 있는 경로는 여러 개가 있으므로(좌상단에서 우하단까지 여러 화살표가 존재하므로), 각 경로가 될 수 있는 확률들을 모두 더해주면 $p(label | \mathbf{x})$, 즉, $p(\mathbf{l} | \mathbf{x})$ 를 구할 수 있다. 이를 수식으로 표현하면 아래와 같다.
$p(\mathbf{l} | \mathbf{x}) = \sum_{\pi \in \mathcal{B}^{-1}(\mathbf{l})}p(\pi | \mathbf{x})$
이때, $\mathcal{B}^{-1}(\mathbf{l})$은 blank token과 중복된 레이블을 제거해서 $\mathbf{l}$이 될 수 있는 모든 가능한 경로들의 집합을 의미한다. 즉, 가능한 모든 경로들이라고 보면 되겠다. 그러나 이렇게 가능한 모든 경로들에 대해 모든 시점, 모든 상태의 확률값을 계산하는 것은 complexity가 매우 높은 연산이다. 가령 time step이 조금 더 길어지거나, 음소의 개수가 늘어난다면 계산 복잡도가 상당히 증가할 것이다. 다행히, CTC 알고리즘은 이를 쉽게 계산할 수 있는 방법이 있다. 바로 Hidden Markov Model(HMM)에서 활용했던 dynamic programming 기법인 forward & backward algorithm을 이용하는 것이다.
Forward & Backward Computation
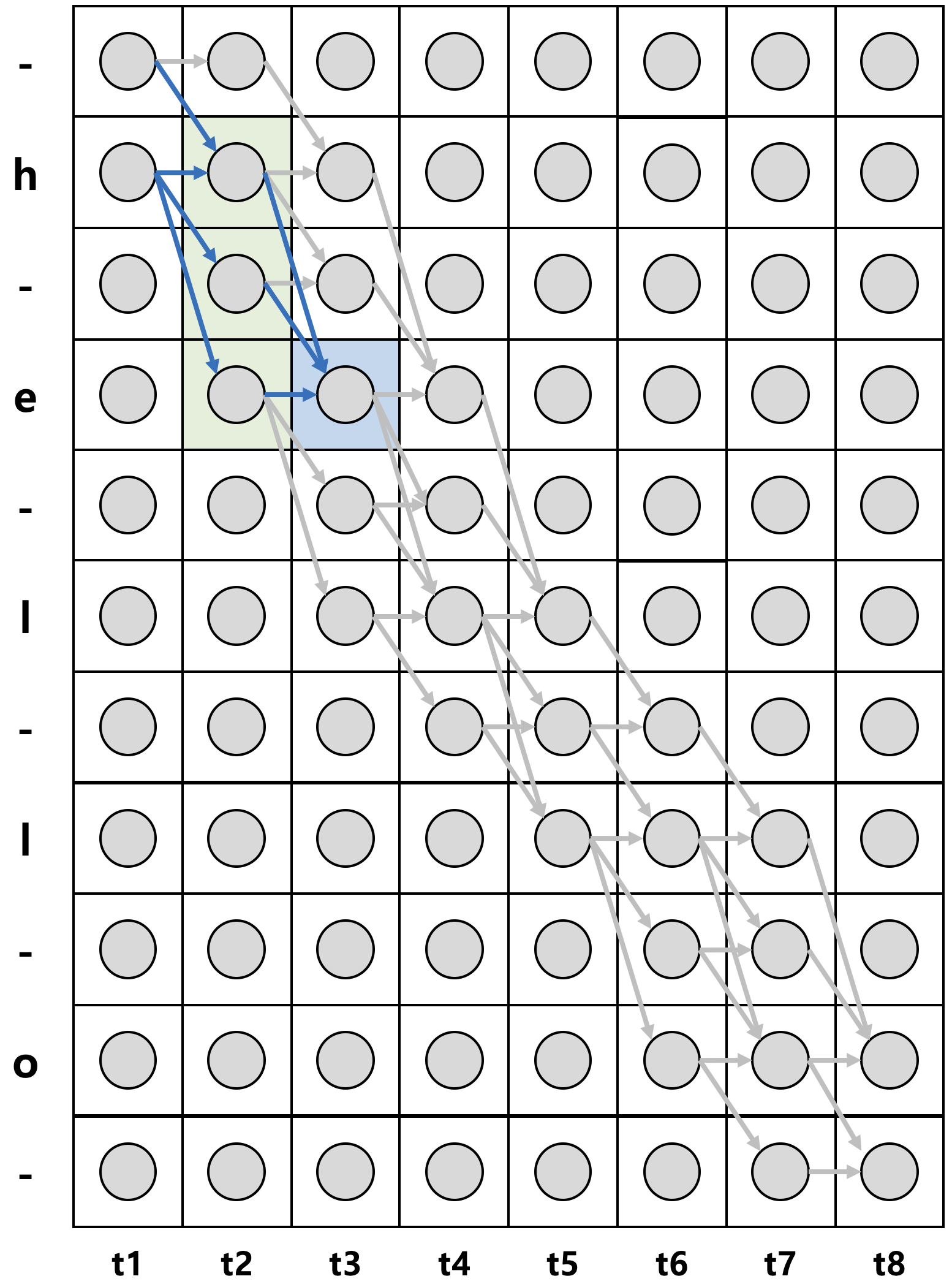
파란색 칸의 전방 확률을 예시로 들어보자. 이 부분은 $\alpha_3(4)$로 표기할 수 있는데, 이 표기는 $t=3$ 시점에 상태 $s=4$(위에서부터 네번째 행, 즉, e)에 있을 전방 확률 $\alpha$라는 뜻이다. 이 곳을 지나는 경로는 -he, hhe, h-e, hee 총 4가지의 경우의 수밖에 없으므로, 이들에 대한 확률을 구함으로써 $\alpha_3(4)$를 구할 수 있다.
$\alpha_3(4)$ = $p$(”-he” | $\mathbf{x}$) + $p$(”hhe” | $\mathbf{x}$) + $p$(”h-e” | $\mathbf{x}$) + $p$(”hee” | $\mathbf{x}$)
$= y^{1}_{−} \cdot y^{2}_{h} \cdot y^{3}_{e} + y^{1}_{h} \cdot y^{2}_{h} \cdot y^{3}_{e} + y^{1}_{h} \cdot y^{2}_{−} \cdot y^{3}_{e}+y^{1}_{h} \cdot y^{2}_{e} \cdot y^{3}_{e}$
이를 일반화한 식은 계산량이 매우 복잡한데, 그 모습은 아래와 같다.
$\alpha_t(s) = \sum_{\pi \in N^T : \mathcal{B}(\pi_{1:t})= \mathbf{l}_{1:t}} \prod_{t’=1}^t y_{\pi_{t’}}^{t’}$
따라서 계산량을 줄이기 위해, 중복되어 사용되는 부분은 미리 계산해두고 추후 이용하는 dynamic programming 기법을 이용한다. 예를 들어, 앞서 파란색 박스 영역인 $\alpha_3(4)$를 구하기 위해 중복 계산되었던 부분은 위 그림에서 초록색 박스 영역에 해당되는 부분($\alpha_2(2)$, $\alpha_2(3)$, $\alpha_2(4)$)이며, 이렇게 중복 사용되는 부분은 미리 계산해두었다가 추후 재사용하면 계산량이 줄어들 수 있다.
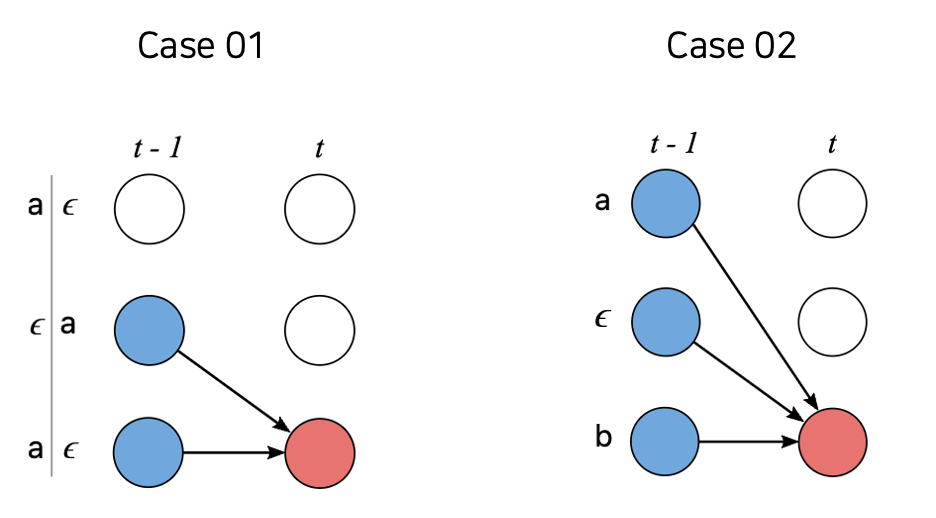
forward algorithm에서 계산을 일반화 할 수 있는 경우는 아래의 case 01과 case 02가 있다. case 01은 $t$시점 현재의 상태가 blank token $\epsilon$이거나, $t$시점 현재의 상태가 전전 시점인 $t$-2의 상태와 동일한 경우이며, case 02는 그 이외의 경우이다. 이를 일반화하면 아래와 같다.
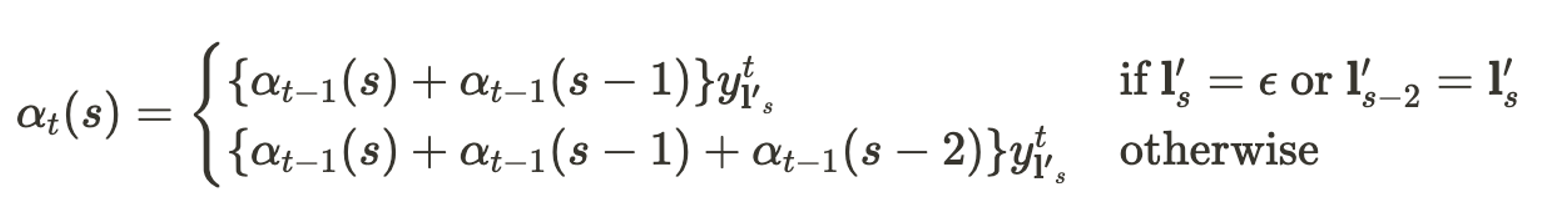
동일한 원리로 backward algorithm 역시 아래와 같이 일반화된다. (자세한 풀이 과정은 생략하고자 하는데, ratsgo’s speech book을 참조하면 좋을 것이다.)
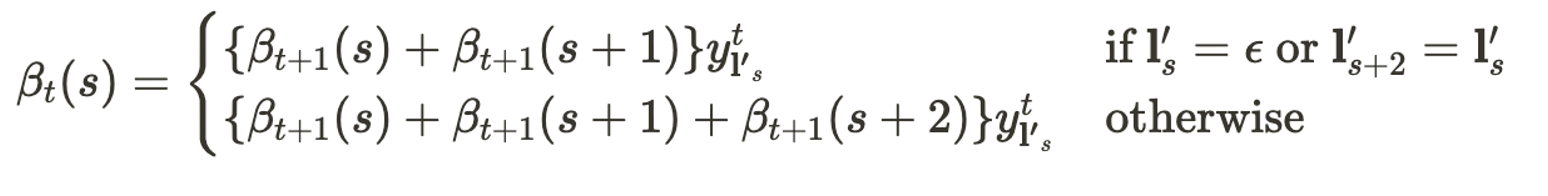
Likelihood Computation
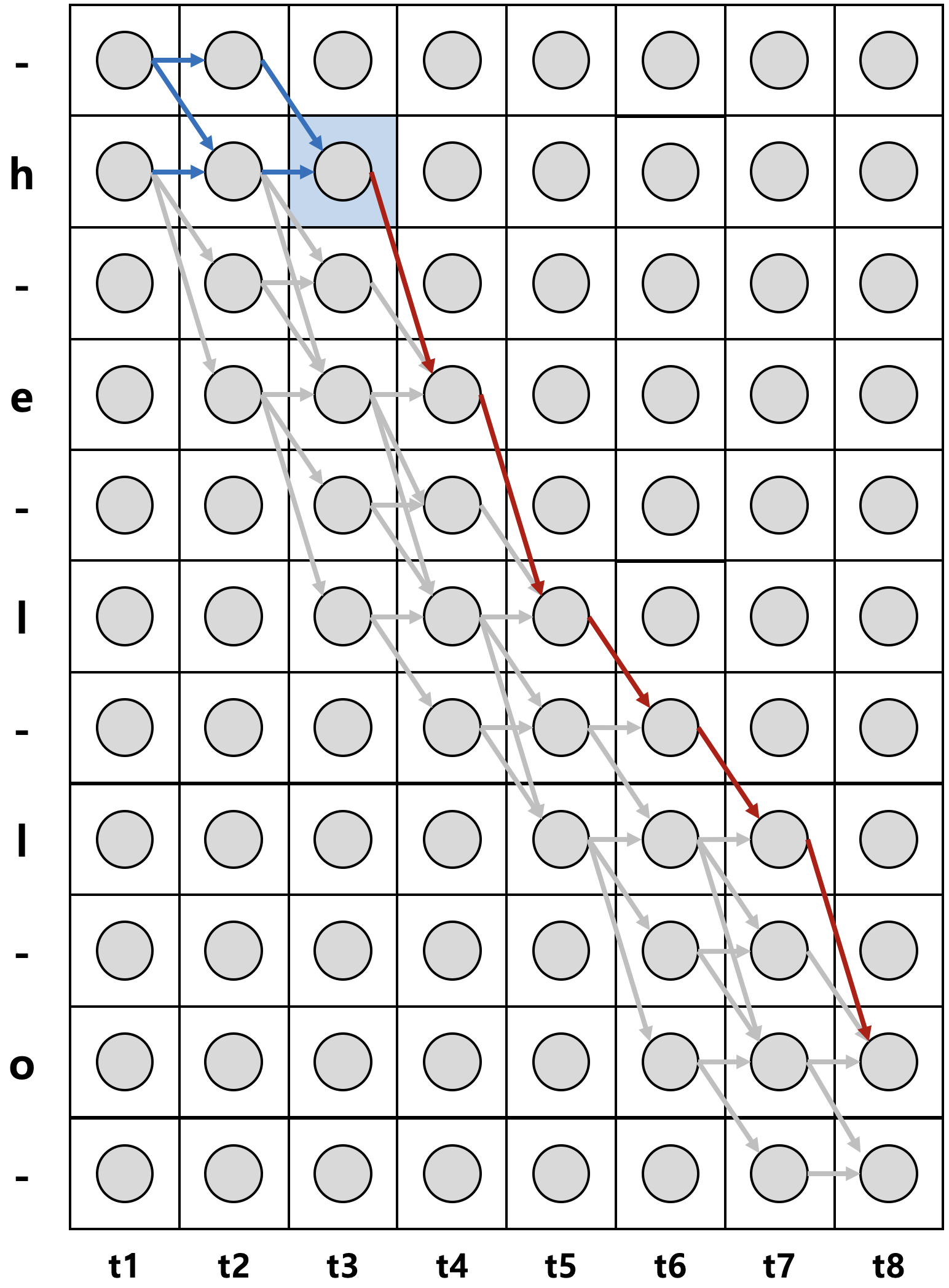
앞서 설명했던 전방확률 $\alpha$와 후방확률 $\beta$를 이용하면 모든 시점과 상태에 대해서 일일이 곱셈을 통해서 확률들을 구하지 않고서도 효율적으로 확률을 계산할 수 있다. 위 그림에서 파란색 칸($t$=3 시점에서 state h)을 반드시 지나면서 h, e, l, l, o로 decoding 될 수 있는 전이 경로에 대한 확률은 $p$(”–hel-lo”|$\mathbf{x}$) + $p$(”-hhel-lo”|$\mathbf{x}$) + $p$(”hhhel-lo”|$\mathbf{x}$)이다. 이를 전방확률과 후방확률로 표현하면 아래와 같이 간단하게 표현될 수 있다.
$\alpha_{3}(2)$ = $p$(”–h”|$\mathbf{x}$) + $p$(”-hh”|$\mathbf{x}$) + $p$(”hhh”|$\mathbf{x}$) = $y^1_−⋅y^2_−⋅y^3_h + y^1_−⋅y^2_h⋅y^3_h + y^1_h⋅y^2_h⋅y^3_h$
$\beta_{3}(2)$ = $p$(”hel-lo”) = $y^{3}_{h} ⋅ y^{4}_{e} ⋅ y^{5}_{l} ⋅ y^{6}_{−} ⋅ y^{7}_{l} ⋅ y^{8}_{o}$
$p$(”–hel-lo”|$\mathbf{x}$) + $p$(”-hhel-lo”|$\mathbf{x}$) + $p$(”hhhel-lo”|$\mathbf{x}$) = $\cfrac{\alpha_{3}(2)\cdot \beta_{3}(2)}{y_{h}^{3}}$
한편, 위와 같이 $t$=3 시점에서 반드시 state h만을 지나야지만 h, e, l, l, o로 decoding 되는 것은 아니다. 아래 그림의 파란색 영역을 지나도 위와 동일하게 h, e, l, l, o로 decoding 될 수 있다.
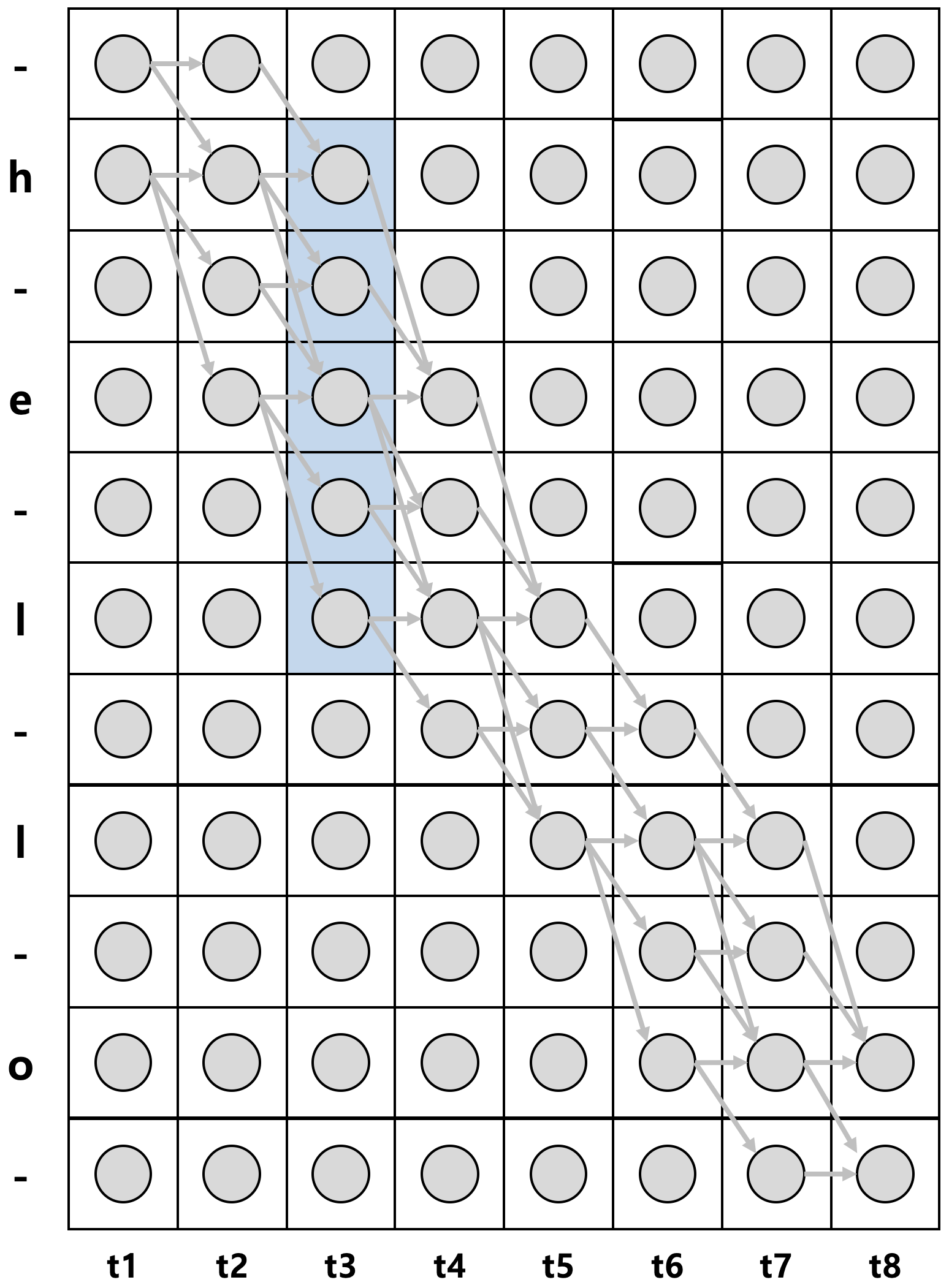
이 또한 전방확률과 후방확률의 곱으로 쉽게 표현될 수 있으며, 이때 계산된 모든 확률들을 모조리 더한 값이 바로 음향 신호 sequence $\mathbf{x}$가 주어졌을 때 h, e, l, l, o로 decoding 될 수 있는 모든 확률의 합, 즉, 우도(likelihood)가 된다.
$p$(”hello” | $\mathbf{x}$) = $\cfrac{\alpha_{3}(2)\cdot \beta_{3}(2)}{y_{h}^{3}}$ + $\cfrac{\alpha_{3}(-)\cdot \beta_{3}(-)}{y_{-}^{3}}$ +$\cfrac{\alpha_{3}(e)\cdot \beta_{3}(e)}{y_{e}^{3}}$ +$\cfrac{\alpha_{3}(-)\cdot \beta_{3}(-)}{y_{-}^{3}}$ +$\cfrac{\alpha_{3}(l)\cdot \beta_{3}(l)}{y_{l}^{3}}$
이를 일반화하여, forward & backward algorithm으로 우도를 도출해내는 수식은 아래와 같다.
$p(\mathbf{l} | \mathbf{x}) = \sum_{s=1}^{|\mathbf{l}’|} \cfrac{\alpha_{t}(s)\cdot \beta_{t}(s)}{y_{\mathbf{l}’_s}^{t}}$
Gradient Computation
앞서 전방확률과 후방확률을 이용하여 우도 $p(label | \mathbf{x})$, 즉, $p(\mathbf{l} | \mathbf{x})$를 유도해냈다. 모델을 학습하기 위해서는 우도를 최대화할 수 있는 모델의 파라미터를 찾아야 한다. 이를 위해서는 우도의 기울기를 구하고, 모델 전체 학습 파라미터에 backpropagation을 수행해야 한다. 보통의 방식처럼, 우도 계산을 로그 우도(log-likelihood, $\ln (p(\mathbf{l} | \mathbf{x}))$)로 수행하는데, 이때 $t$번째 시점 $k$번째 음소에 대한 로그 우도의 기울기는 아래와 같다.
$\cfrac {\partial \ln (p(\mathbf{l}| \mathbf{x})))} {\partial y_k^t} = \cfrac{1}{p(\mathbf{l}|\mathbf{x})} \cfrac{\partial p(\mathbf{l}|\mathbf{x})}{\partial y_k^t} = \cfrac{1}{p(\mathbf{l}|\mathbf{x})} \left( -\cfrac {1}{(y_k^t)^2} \sum_{s \in lab(\mathbf{l}, k)} \alpha_{t}(s) \cdot \beta_{t}(s)\right)$
- 합성함수 미분법$f{g(x)} \prime = f \prime(g(x)) g\prime(x)$ 및 $\ln(x)$를 $x$로 미분하면 1/$x$ 임을 참고하여, $\ln (p(\mathbf{l} | \mathbf{x}))$를 합성함수로 보면 아래가 성립됨
- $\cfrac {\partial \ln (p(\mathbf{l}| \mathbf{x})))} {\partial y_k^t} = \cfrac{1}{p(\mathbf{l}|\mathbf{x})} \cfrac{\partial p(\mathbf{l}|\mathbf{x})}{\partial y_k^t}$
- 상수 $a$에 대해 $a$/$x$를 $x$로 미분하면 $-a$/$x^2$라는 점을 고려하여, 아래가 성립됨
- $p(\mathbf{l} | \mathbf{x}) = \sum_{s=1}^{|\mathbf{l}’|} \cfrac{\alpha_{t}(s)\cdot \beta_{t}(s)}{y_{\mathbf{l}’_s}^{t}}$ 이므로,
- 이때 $lab(\mathbf{l},k)$는 k라는 음소 레이블이 $\mathbf{l}’$에서 나타난 위치를 의미함
즉, 복잡하지만 모델 파라미터에 대한 로그 우도의 기울기는 전방확률과 후방확률을 이용한 식으로 계산할 수 있다. 이를 이용하여 backpropagation을 수행하는 것이 CTC 알고리즘의 학습 방식이다.
Rescaling
한편, CTC 저자에 따르면, 전방확률과 후방확률의 계산 과정에서 그 값이 너무 작아져 underflow 문제가 발생할 수 있다고 한다. 따라서 이를 방지하기 위해 다음과 같이 rescailing을 한다.
- 전방확률에 대한 rescailing
- $C_t = \sum_s \alpha_t (s)$
- $\hat \alpha_t(s) = \cfrac{\alpha_t (s)}{C_t}$
- 후방확률에 대한 rescailing
- $D_t = \sum_s \beta_t (s)$
- $\hat \beta_t(s) = \cfrac{\beta_t (s)}{D_t}$
Decoding
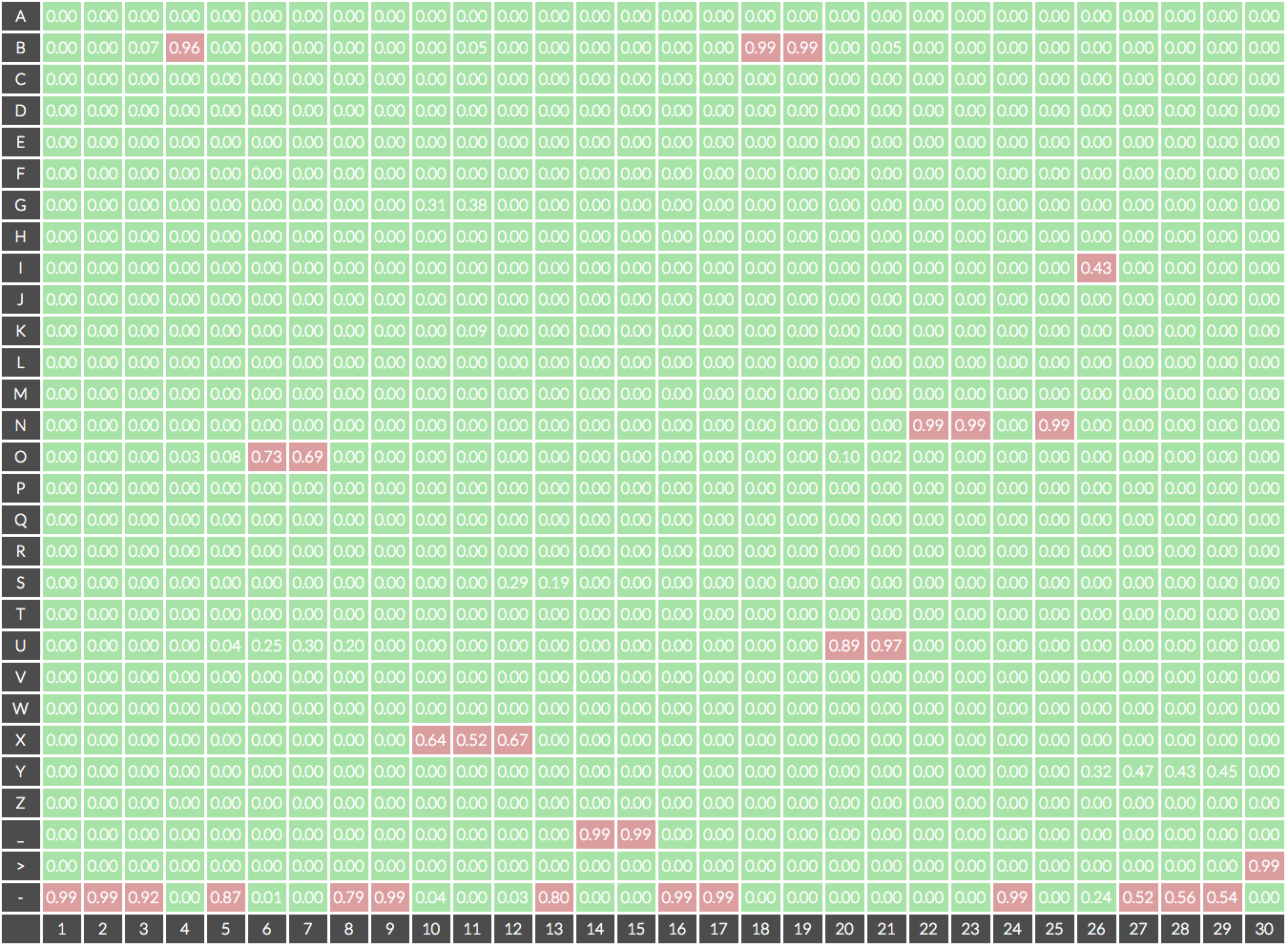
CTC 알고리즘은 일종의 손실이라고 했다. 이를 활용하여 학습한 모델은 음향 신호 sequence $\mathbf{x}$가 주어졌을 때 위와 같이 각 time step마다 ‘음소 개수 + 1(blank token $\epsilon$)’개 차원의 확률 벡터를 출력한다. 이때, 각 time step마다 가장 높은 확률에 해당하는 음소를 선택하여 decoding 하는 방식을 Best Path Decoding이라고 한다. 이 예에서는 ---B-OO--XXX-__--BBUUNN-NI---> , 즉 BOX_BUNNI로 decoding 된다.
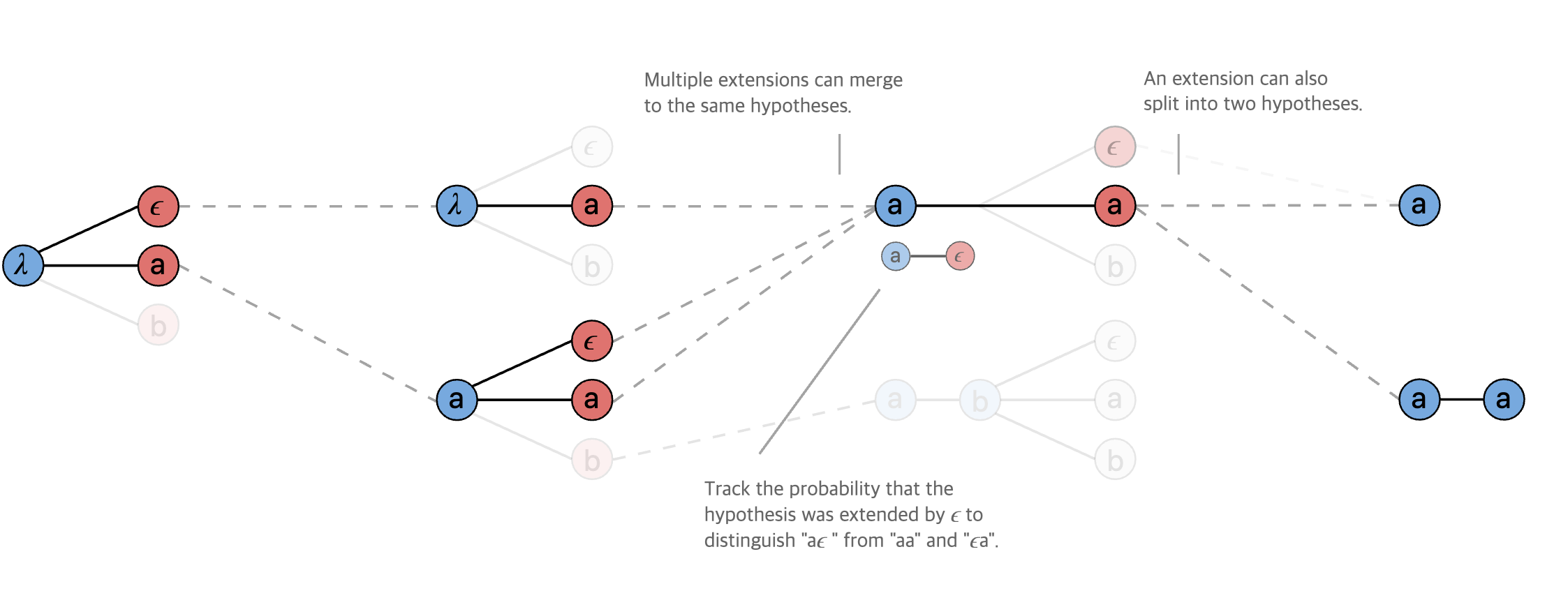
반면, 위와 같이 Beam Search를 decoding에 적용하는 것 또한 가능하다. 이는 beam size(가령, beam size=3)를 정해두고, 매 time step마다 beam size만큼 가장 확률이 높은 후보 sequence를 남겨가며 decoding 하는 방식이다.
04. 정리하며
음향 신호 sequence와 이에 대한 음소의 명시적인 정렬 관계를 정의하지 않고서도 뉴럴 네트워크가 이를 학습할 수 있는 방식인 CTC 알고리즘을 살펴보았다. cross entropy를 손실함수로 쓰지 않기 때문에 우도를 구하는 과정에서 복잡한 forward & backward 알고리즘을 사용했다.
CTC 알고리즘은 음향 신호와 음소 간 명시적인 정렬 관계를 만들기 위해 레이블을 만드는 공수는 필요가 없다는 장점이 있다. 그러나, 그만큼 학습이 수렴하는 데 어려움이 있어서 명시적인 정렬 관계와 cross entropy 손실함수를 사용하는 모델 대비 많은 학습 데이터가 필요하다는 단점이 있다고 한다. 또한 언어모델 도움 없이는 decoding 품질이 좋지 않을 수 있다는 단점 또한 존재한다.
05. 참고 문헌
[1] Graves, Alex, et al. “Connectionist temporal classification: labelling unsegmented sequence data with recurrent neural networks.” Proceedings of the 23rd international conference on Machine learning. 2006.
[2] Sequence Modeling With CTC
[3] ratsgo 님의 블로그