이 포스트는 개인적으로 공부한 내용을 정리하고 필요한 분들에게 지식을 공유하기 위해 작성되었습니다. 지적하실 내용이 있다면, 언제든 댓글 또는 메일로 알려주시기를 바랍니다.
01. 개요
VQ-Wav2Vec의 핵심은 Wav2Vec에 Vector Quantization을 적용하였다는 점이다. VQ-Wav2Vec은 Wav2Vec 방식과 유사한 self-supervised context prediction task를 수행하며 학습되는데, continuous한 음성 신호의 세그먼트(segments)를 quantization(양자화) 함으로써 discrete한 representation으로 학습하는 방식을 제안한다. 이러한 discretization은 Gumbel-Softmax와 k-means 클러스터링을 통해서 수행할 수 있다.
왜 굳이 discretization을 수행하는 것일까? BERT와 같은 NLP 태스크에서는 입력되는 단어들의 시퀀스가 discrete한데, VQ-Wav2Vec 방식으로 discretization을 수행하면 이산화된 음성 신호를 BERT 같은 모델에 직접 입력값으로 사용할 수 있을 것이라는 아이디어에서 착안된 것이다.
실제로 VQ-Wav2Vec 저자들은 실험을 통해서 BERT와 함께 학습하여 TIMIT 음소 분류 문제 및 WSJ 음성 인식 문제에서 새로운 SOTA를 달성했다고 주장한다.
02. VQ-Wav2Vec의 학습
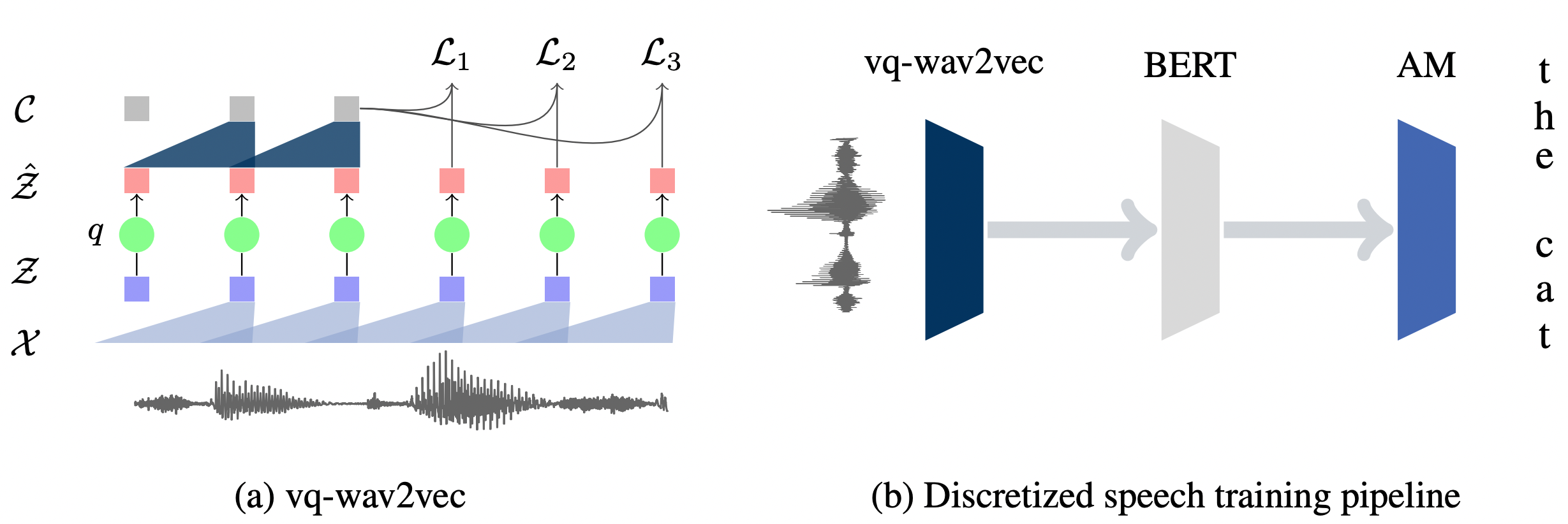
VQ-Wav2Vec은 기본적으로 Wav2Vec과 동일한 방식으로, negative 오디오 샘플로부터 true 오디오 샘플을 구별해내는 contrastive loss를 최소화하며 학습한다.
새롭게 추가된 부분이 있다면, 위 그림 (a)에서 연두색 $q$ 부분이다. 기존 Wav2Vec에서는 encoder network인 $f:\mathcal{X} \mapsto \mathcal{Z}$와 context network인 $g:\mathcal{\hat{Z}} \mapsto \mathcal{C}$가 컨볼루션 네트워크로 구성되어 있을 뿐이었다.
VQ-Wav2Vec에서는 새롭게 quantization module $q:\mathcal{Z} \mapsto \mathcal{\hat{Z}}$이 추가되었다. 즉, encoder network $f$는 30ms의 원시 음성 신호를 10ms의 dense representation $\mathbf{z}$로 인코딩하는데, quantizer $q$에 의해 dense representation $\mathbf{z}$가 discrete한 원 핫 벡터(one-hot vector)로 바뀌게 된다. 최종적으로 이러한 one-hot 벡터를 이용하여 다시금 dense representation $\mathbf{\hat{z}}$를 복원해낸다. 이처럼 dense representation $\mathbf{z}$를 discrete한 one-hot 벡터로 바꾸는 방법은 Gumbel-Softmax를 활용하는 방법과 K-means 클러스터링을 활용하는 방법이 있다. 이후 과정을 Wav2Vec과 동일하게 학습한다.
Gumbel-Softmax를 활용한 방법
Gumbel-Softmax에 대한 간단한 개념
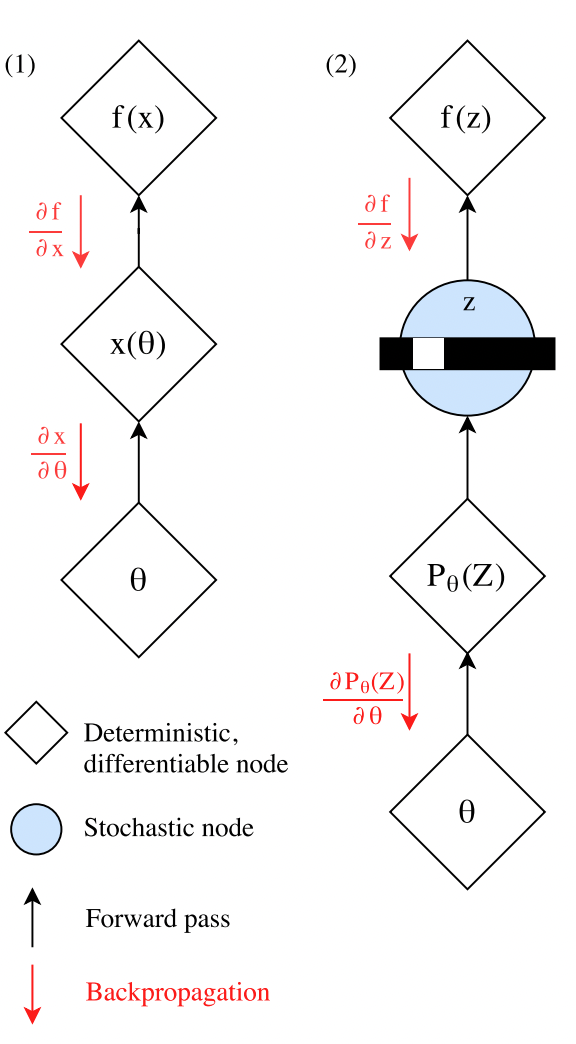
우선 Gumbel-Softmax를 간단하게 살펴보자. 위의 그림 (1)과 같은 일반적인 뉴럴 네트워크 구조에서 $\mathbf{x}(\theta)$와 같이 deterministic 하며 미분 가능한 노드에서는 체인 룰에 의해서 backpropagation을 수행할 수 있다. 반면, (2)와 같이 중간에 한 노드에서 softmax - argmax 등을 거쳐 categorical 변수들에 대해 sampling을 수행하는 노드는 stochastic한 요소가 들어가게 되어 backpropagation을 수행할 수 없게된다.
이러한 문제를 해결하기 위해 Gumbel-Softmax는 확률적으로 sampling을 할 수 있으면서도 backpropagation이 가능한 방식을 제시한다. 원 논문의 설명은 장황하지만, VQ-Wav2Vec 논문을 참고하여 간단하게 아래와 같이 정리할 수 있다.
[수식 1] $p_j=\cfrac{\exp{(l_j+v_j)/\tau}}{\sum_{k=1}^{V}\exp{(l_k+v_k)/\tau}}$
각 notation에 대한 설명은 다음과 같다.
- $l \in \mathbb{R}^V$은 encoder network를 거쳐서 나온 dense representation $\mathbf{z}$에 대해 linear layer와 ReLU, 그리고 또 한번의 linear layer를 통과한 로짓값이다.
$u$는 uniform distribution $U(0, 1)$에서 랜덤하게 sampling한 값들이며, 이를 활용하여 log 연산을 취함으로써 다음과 같이 $v = -\log(-\log(u))$를 정의한다. 이를 코드로 보면 아래와 같다.
1 2 3 4 5 6 7 8
import torch import torch.nn as nn import torch.nn.functional as F from torch.autograd import Variable def sample_gumbel(shape, eps=1e-20): U = torch.rand(shape).cuda() return -Variable(torch.log(-torch.log(U + eps) + eps))
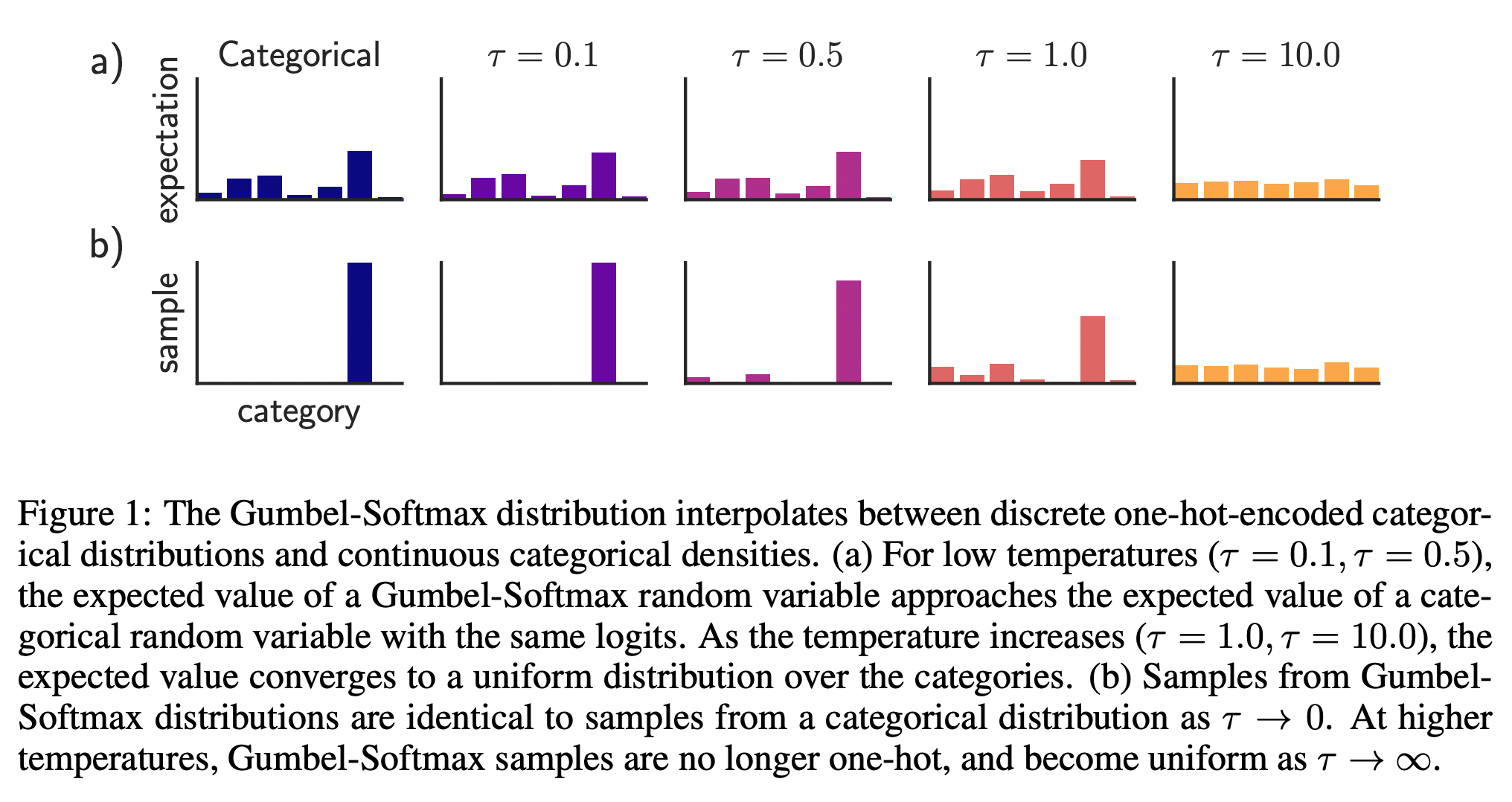
$\tau$는 temperature로 불리는데, 이 값이 0에 가까울수록 one hot 벡터처럼 categorical한 분포를 가지게되며, 값이 클수록 uniform한 분포를 가지게 된다.
![fig03]()
$p_j$를 코드로 보면 아래와 같다.
1 2 3
def gumbel_softmax_sample(logits, temperature): y = logits + sample_gumbel(logits.size()) return F.softmax(y / temperature, dim=-1)
앞서 Gumbel-Softmax의 핵심은 softmax-argmax 등의 stochastic 연산을 뉴럴 네트워크 내 노드에서 수행하여도 backpropagation이 가능해진다고 했다. 이에 대해서는 아래와 같은 트릭이 적용된다.
1
2
3
4
5
6
7
8
9
10
11
12
def gumbel_softmax(logits, temperature):
"""
input: [*, n_class]
return: [*, n_class] an one-hot vector
"""
y = gumbel_softmax_sample(logits, temperature)
shape = y.size()
_, ind = y.max(dim=-1)
y_hard = torch.zeros_like(y).view(-1, shape[-1])
y_hard.scatter_(1, ind.view(-1, 1), 1)
y_hard = y_hard.view(*shape)
return (y_hard - y).detach() + y
이 때의 return 값을 주목해보겠다. 순전파 연산에서는 (-y).detach() + y로 y는 소거되고, 결과적으로 softmax 연산을 통해 구한 one-hot 벡터인 y_hard 변수가 return된다. 한편, backpropagation 연산에서는 .detach() 함수가 적용되어 있지 않은 y에 대해서만 gradient가 흘러갈 수 있게된다. 즉, backpropagation이 가능한 것이다!
Gumbel-Softmax를 활용한 VQ-Wav2Vec 학습
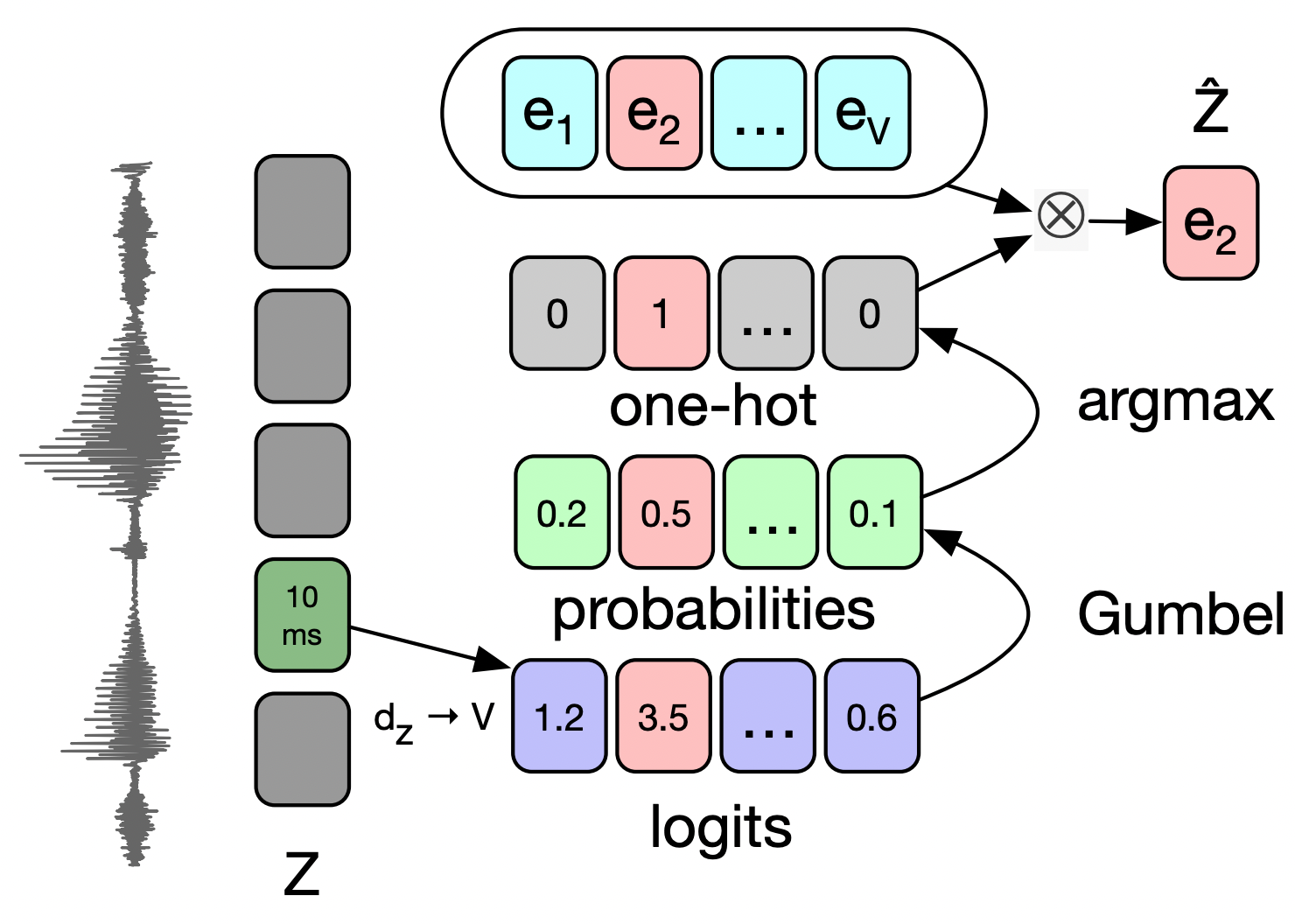
quantizer $q$에 의해서, 10ms로 인코딩된 dense representation $\mathbf{z}$는 위의 과정을 거쳐 discrete한 one-hot 벡터로 바뀌게 된다. 이제 이 one-hot 벡터는 codebook이라 불리는 임베딩 행렬 $\mathbf{e} \in \mathbb{R}^{V \times d}$와 곱해짐으로써 $\mathbf{\hat{z}}=\mathbf{e}_i$벡터를 얻게 된다.
K-means 클러스터링을 활용한 방법
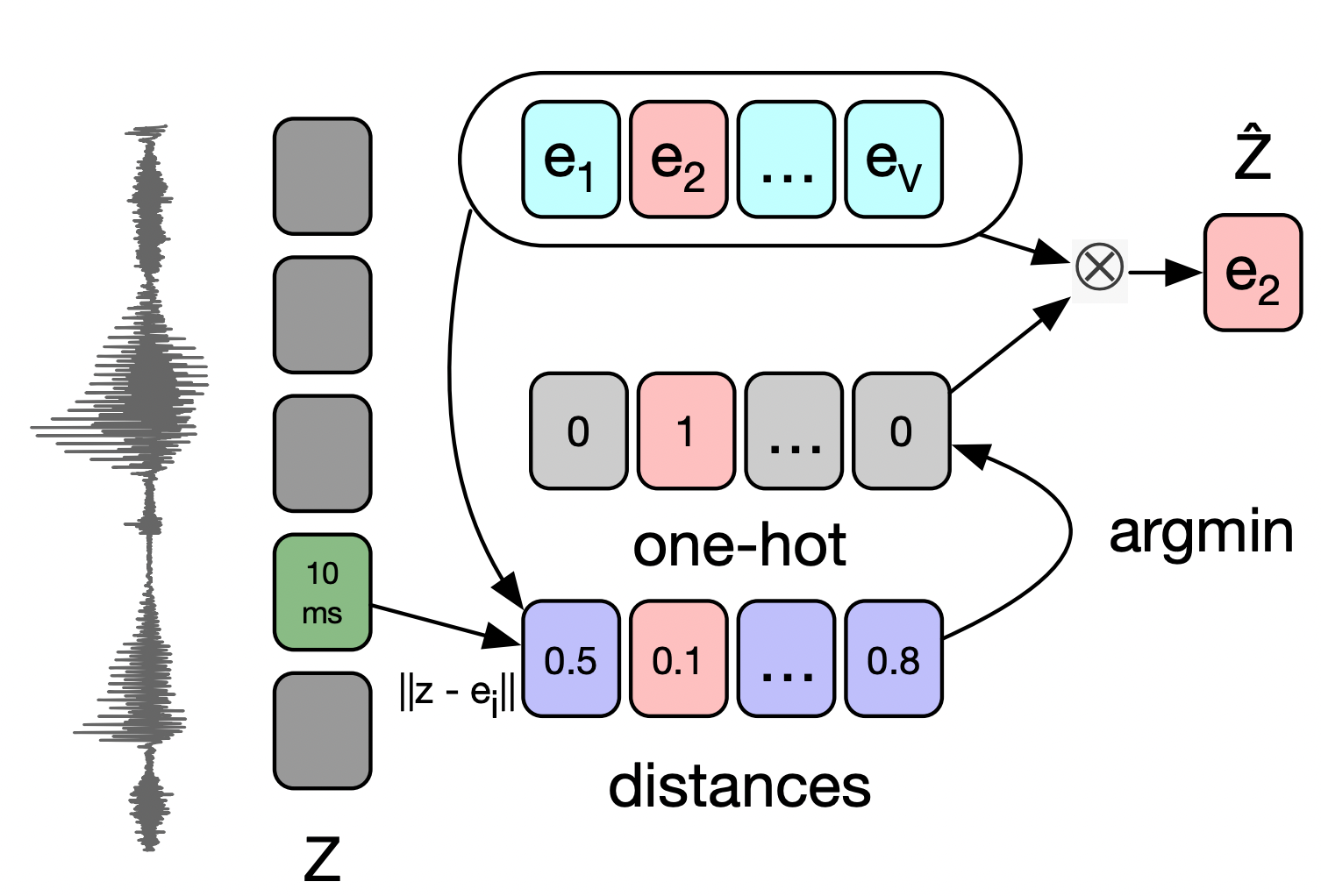
앞서 살펴보았던 Gumbel-Softmax를 활용한 방식은 결국 벡터를 quantization하기 위한 트릭이었다. 이에 대한 대안으로 저자는 K-means 클러스터링을 활용하는 방식도 제안하였는데, 이는 encoder network의 출력인 10ms의 벡터 $\mathbf{z}$와 임베딩 행렬 내의 벡터 $\mathbf{e}$들 간 유클리디안 거리를 계산하고, 이와 가장 가까운 벡터를 활용하여 $\mathbf{\hat{z}}=\mathbf{e}_i$벡터를 얻는 방식이다. 이러한 방식도 미분 불가능한 $\arg \min$연산을 포함하지만, Gumbel-Softmax 때와 같이 역전파 과정을 섬세히 설계함으로써 backpropagation이 가능하도록 설정할 수 있다.
03. VQ-Wav2Vec을 접목한 BERT 사전 학습
VQ-Wav2Vec의 학습을 마치고 나면, discretization이 적용된 오디오 데이터 특징을 추출할 수 있다. 이러한 discrete 입력값은 MLM 방식으로 학습하는 BERT의 사전 학습에 활용될 수 있다. 즉, BERT를 이용해서 입력값에 대한 양방향의 맥락을 학습하는 것이다.
BERT의 사전 학습을 마치고 나면, discrete 입력값이 BERT에 입력되었을 때, 양방향 맥락이 고려된 representation들이 추출될 수 있는데, 이는 곧 speech recognition 태스크의 음향 모델의 입력값이 될 수 있다.
04. 참고 문헌
[1] Baevski, Alexei, Steffen Schneider, and Michael Auli. “vq-wav2vec: Self-supervised learning of discrete speech representations.” arXiv preprint arXiv:1910.05453 (2019).
[2] ratsgo 님의 블로그
[3] 김정희 님의 발표자료