Matrix Factorization Techniques for Recommender Systems

이 포스트는 개인적으로 공부한 내용을 정리하고 필요한 분들에게 지식을 공유하기 위해 작성되었습니다.
지적하실 내용이 있다면, 언제든 댓글 또는 메일로 알려주시기를 바랍니다.

본 포스트 내용은 Matrix Factorization Techniques for Recommender Systems을 번역한 글입니다.

00. Abstract

Netflix Prize competition에서 알 수 있듯, matrix factorization 기법은 implicit feedback, temporal effects, confidence level 등 부수적인 정보들을 아우를 수 있다는 점에서 전통적인 방식보다 제품을 추천하는 데 용이하다.

01. Recommender System Strategies

01-1. 추천시스템의 두 종류 : content filtering과 collaborative filtering

추천시스템은 크게 content filtering과 collaborative filtering 두 종류로 구분할 수 있다.

먼저, content filtering 방식부터 살펴보자. content filtering 방식은 콘텐츠가 유저에게 잘 추천될 수 있도록, 유저에 대한 profile과 콘텐츠에 대한 profile을 만들어 활용한다. 예를 들어, ‘유저’ profile의 경우, 인구통계학적 정보라든지 어떤 설문에 대한 답변 등으로 구성할 수 있을 것이다. 또한 ‘영화’ 콘텐츠의 profile 경우, 장르, 출연배우, 인기도, … 등으로 구성할 수 있을 것이다. 프로그램은 이렇게 구성한 profile 들을 기반으로 유저와 콘텐츠(product)를 매칭시키는 것이다. 물론, 이러한 content-based 전략도 위처럼 정의한 profile 정보 이외에도 쉽게 수집하기 어려운 외부 정보들까지 활용하기도 한다.

content filtering 방식을 성공적으로 구현한 대표적인 사례로는 인터넷 라디오 서비스인 Pandora.com에서 활용되었던 Music Genome Project가 있다. 이를 구현하기 위해서, 숙련된 음악 분석가가 Music Genome Project의 음악들을 수백여개의 음악적 특징들을 기반으로 하여 스코어링을 했었다. 이렇게 구성한 정보들은 각 곡의 음악적 특징 뿐만 아니라, 청취자의 음악적 취향과 상당한 관계가 있는 요소들까지도 아우른다.

위와 같은 content filtering 방식은 explicit한 profile을 만들어야만 한다. 이에 반해, content filtering의 대안이 되는 collaborative filtering 방식은 explicit한 profile 대신, 유저의 지난 거래정보나 평점 등 과거 행동만을 활용하여 추천한다. 즉, 특정 제품에 대하여 유저가 매겼던 평점 등 과거 정보와 해당 유저 사이의 상호관계성을 분석하고, 이를 토대로 새로이 유저-아이템 간의 관계를 발견하는 것이다.

collaborative filtering은 특정 도메인에 종속되지 않을 뿐만 아니라, explicit한 profile을 구성하지 않아도 되기 때문에 profile을 구성해야만 하는 content filtering 방식의 한계를 극복할 수 있는 장점이 있다. 한편, content-based 방식보다 잘 작동한다는 장점이 있지만, 새로운 제품과 유저 간의 관계를 시스템이 알기 어렵기 때문에 `cold start 문제가 존재한다는 단점도 있다.

01-2. Collaborative filtering의 두 종류 : neighborhood methods와 latent factor models

collaborative filtering은 neighborhood methods와 latent factor model로 구분지어 볼 수 있다.

먼저, neighborhood methods` 아이템들끼리의 이웃관계 또는 유저들끼리의 이웃관계를 중점적으로 고려한다. 아이템끼리의 관계를 고려하는 경우, 동일한 유저에 의해 평점이 매겨진 ‘이웃 아이템’들에도 유저의 선호도가 반영되어 있다고 본다. 즉, 동일한 유저에 의해서 유사한 평점을 받을 가능성이 있는 제품이 바로 ‘해당 제품의 이웃’이 되어 추천되는 것이다. ‘라이언 일병 구하기’를 예로 들어보자. 이 영화의 이웃은 전쟁 영화일수도, 스필버그의 영화일수도, 톰 행크스의 영화일수도 , …, 있을 것이다. 그래서 라이언 일병 구하기에 대한 해당 유저의 평점을 예측하기 위해서는 이 유저가 실제로 매긴 최근접 이웃 영화들을 살펴보아야 한다.

유저들끼리의 이웃관계를 고려할 경우, 아래 그림처럼 유저들이 서로의 평점 정보를 보완해줄수도 있다.

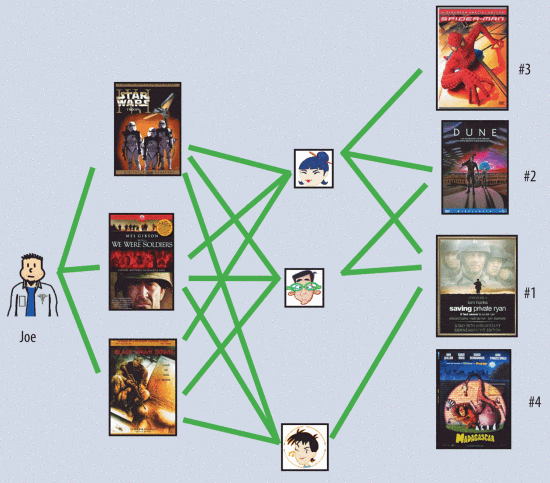
즉, 위 그림을 해석해보자면, Joe가 왼쪽 세 영화를 좋아하는 경우 Joe를 위한 추천을 하고자 한다면, 추천시스템은 ‘Joe가 좋아한 세 영화를 모두 좋아하는 유저’들을 ‘Joe와 유사한 유저’로 간주하여 그들이 좋아한 영화를 추천할 것이다. 여기서는 Joe가 좋아하는 영화를 모두 본 3명의 유저 중 2명이 좋아한 영화 Dune이 Joe에게 추천될 것이다.

latent factor models는 사용자와 아이템을 잠재적인 요인(factor)들을 사용해서 나타낼 수 있다고 보는 모델로 neighborhood methods의 대안이 된다. 어떤 의미로 본다면, 위 content filtering 방식에서 숙련된 음악 분석가가 직접 음악의 특징들을 고려하여 평점을 매겼던 것을 대체하는 방식이라고 볼수도 있겠다. 영화를 예로 든다면, 이 factor들은 어떤 장르인지, 액션 요소는 얼마나 많은지, 아이들이 볼 수 있는 영화인지 등을 나타낼 것이고, 하나의 차원(dimension)으로써 표현될 것이다. 또한, 만약 유저로 예로 든다면, 각각의 factor들은 특정 유저가 해당 영화를 얼마의 score 만큼 좋아하는지를 표현한다고 볼 수 있겠다.

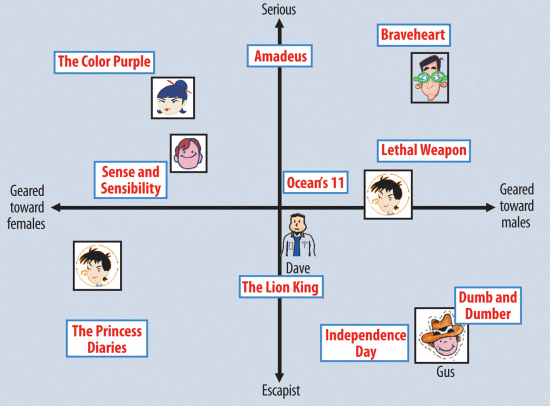
아래 그림은 두 차원으로 간단하게 latent factor models의 아이디어를 표현한 것이다. 한 축은 여성-남성을 나타내는 차원의 축이고, 다른 한 축은 현실적(serious)-이상적(escapist) 성향을 나타내는 차원의 축이다. 이러한 모델에서는, 어떤 영화에 대해서 유저가 예측한 평균 평점은 그래프 상에서 영화와 유저의 벡터 내적이라고 볼 수 있겠다. 예를 들어, Gus는 영화 Dumb and Dumber를 좋아할 것으로 보이고, The Color Purple은 싫어할 것으로 보인다. 영화 Oceans 11과 유저 Dave는 두 차원의 중간 쯤 위치한 것으로 보아, 두 차원에 대해서는 중립적인 성향을 보이는 것으로 해석할 수 있다.

02. Matrix Factorization Methods

latent factor 모델을 가장 성공적으로 구현한 사례가 바로 matrix factorization 모델이다. matrix factorization 모델은 아이템 평점 패턴으로부터 추론된 요인 벡터로 유저와 아이템을 표현하며, 유저와 아이템 요인 간 상호관계가 높을 때 추천으로 이어지게 된다. matrix factorization은 정확도가 높으며 확장성이 뛰어나서 많이 활용되는 방식이며, 무엇보다도 현실세계의 상황을 모델링하는 데 유연성있게 적용될 수 있어서 매우 효과적이다.

추천시스템의 입력 데이터는 유저를 나타내는 차원과 아이템 선호도를 나타내는 다른 차원으로 구성된 행렬로 이루어져 있다. 추천시스템 데이터로 활용하기에 가장 편리한 데이터는 단연코 유저가 특정 제품에 자신의 선호도를 대놓고 표현한, 높은 퀄리티의 explicit feedback일 것이다. 이러한 데이터를 수집하기 위해서 많은 기업들이 별점과 좋아요 등을 수집하는 것이다. 그런데 대개, explicit feedback을 표현하는 행렬은 sparse하다. 왜냐하면 대부분의 유저들은 전체 수많은 아이템들 중 매우 일부분에 대해서만 평점을 부여하기 때문이다.

matrix factorization의 가장 큰 강점 중 하나는 explicit feedback 이외의 여러 부가정보들을 통합하여 활용할 수 있다는 점이다. explicit feedback을 수집하기 어려운 상황에서, 추천시스템은 유저의 행동, 구매 내역, 검색 내역, 검색 패턴, 마우스의 움직임 등 implicit feedback으로 유저의 선호를 파악할 수 있다. 이러한 implicit feedback은 일반적으로 dense한 행렬로 표현될 수 있다.

03. A Basic Matrix Factorization Model

matrix factorization models는 유저-아이템을 $f$ 차원의 joint latent factor space(결합 잠재 요인 공간)에 근사한다. 이때, 유저와 아이템 간 상호작용은 공간 상에서 두 벡터의 내적으로 모델링된다. 즉, 각각의 아이템 $i$는 벡터 $q_i∈ℝ^f$로 표현되며, 각각의 유저는 벡터 $p_u∈ℝ^f$로 표현된다. 아이템 $i$ 에 대하여, 벡터 $q_i$의 element들은 해당 item들이 얼마나 긍정적인지, 부정적인지를 나타낸다고 볼 수 있다. 마찬가지로, 유저 $u$ 에 대하여, 벡터 $p_u$의 element들은 해당 유저가 얼마나 해당 아이템을 선호하는지, 긍부정의 정도를 내포하고 있다. 따라서 두 벡터의 내적 $q^T_ip_u$는 유저 $u$와 아이템 $i$의 상호작용(interaction), 즉, 유저 $u$의 아이템 $i$에 대한 전반적인 선호도를 내포한다고 볼 수 있겠다. 이렇게 구한 평점에 대한 추정값을 수식으로 표현하면 아래와 같다.

💡 (수식 1) $\hat{r}_{ui}=q^T_ip_u$

그렇다면, 각각의 아이템과 유저를 요인 벡터 $q_i,p_u∈ℝ^f$로 어떻게 mapping 할까? 이러한 mapping 작업만 잘 마무리할 수 있다면, 추천시스템은 어떠한 아이템이든 유저가 매길 평점을 쉽사리 예측해낼 수 있을텐데 말이다.

그 방법은 information retrieval(IR) 분야에서 latent semantic factor를 발견하는 데 활용되는 기술인 singular value decompoistion(SVD) 모델과 큰 관련이 있다. 하지만 문제가 있다. SVD를 collaborative filtering 도메인에 적용하기 위해서는 유저-아이템 평점 행렬을 factoring 해야하지만, 유저-아이템 행렬은 sparse한 경우가 매우 많아서 전통적인 SVD를 그대로 적용하기 어렵기 때문이다. 그리고 행렬 내 우리가 알고 있는 정보들만을 대상으로 적용한다고 하더라도 과적합이 일어나기 일쑤다.

기존 시스템은 비어있는 평점들을 채워서 평점 행렬을 최대한 dense하게 만들어 활용하려고 노력했다. 그러나, 이러한 방법은 데이터가 상당히 많아진 오늘날 적용하기에 대단히 수고로운 작업일 것이다. 정확하지 않은 방식으로 행렬을 dense하게 채워넣는 것은 상당한 정보를 왜곡하는 행동이기도 하다. 따라서 최근에는 관측된 평점만을 직접 활용하되, 과적합을 줄일 수 있는 정규화(regularized) 모델을 활용한다. 따라서 요인 벡터 $q_i,p_u∈ℝ^f$를 학습하기 위해서, 추천시스템은 관측된 평점들에 대해서 regularized squared error를 최소화 하는 방식을 활용한다.

💡 (수식 2) $\min\limits_{q^{\star},p^{\star}}\sum\limits_{(u,i)\in \kappa}(r_{ui}-q_{i}^{T} p_{u})^{2}+\lambda(\lVert q_{i}\rVert^{2}+\lVert p_{u}\rVert^{2})$

이때, $κ$는 평점을 알고 있는 $r_{ui}$에 대한 학습데이터 $(u, i)$ 쌍의 셋이다.

추천시스템은 과거로부터 관측된 평점으로 모델을 학습한다. 그런데 우리가 풀고자 하는 문제는 이를 일반화하여 미래에 미지의 평점을 예측하는 것이다. 따라서 추천시스템은 정규화를 통해서 과적합을 피하는 방식으로 학습을 하는데, 위 수식에서 상수 $\lambda$가 정규화의 강도를 조정하는 상수가 되겠다.

04. Learning Algorithms

(수식 2)를 최소화 하는 방법으로는 stochastic gradient descent(SGD)와 alternating least squares(ALS) 두 가지가 있다.

04-1. Stochastic Gradient Descent

먼저, prediction error는 아래와 같이 평점을 알고 있는 $r_{ui}$와 유저 및 아이템의 요인벡터를 내적한 값의 차이로 정의한다.

💡 (수식 3) $e_{ui}\,\overset{def}{=}\,r_{ui}-q^T_ip_u$

이를 참고하여 아래와 같이 학습률 $\gamma$의 정도만큼 기울기의 반대 방향으로 파라미터를 변경해간다.

💡 (수식 4) $q_i \leftarrow q_i + \gamma \cdot (e_{ui} \cdot p_u - \lambda \cdot q_i )$
💡 (수식 5) $p_u \leftarrow p_u + \gamma \cdot (e_{ui} \cdot q_i - \lambda \cdot p_u )$

이 방식은 상대적으로 빠른 running time으로 구현이 가능하지만. 때로는 ALS 최적화 기법이 유리할 때도 있다.

04-2. Alternating Least Squares

요인 벡터 $q_i,p_u$는 미지수이므로 convex하지 못하다. 그러나 두 미지수 중 하나를 고정한다면, 최적화 문제는 2차(quadratic)식 문제가 되어 최적으로 풀 수 있게 된다. 따라서 ALS 기법은 $q_i$와 $p_u$를 번갈아가며 고정하여 문제를 푼다. 예를 들어, $p_u$를 고정할 땐 $q_i$를 least square 문제로 계산한다. 이러한 방식으로 (수식 2)가 최소로 수렴할 수 있다.

05. Adding Biases

collaborative filtering에서 matrix factorization을 활용하는 데 이점으로는 다양한 데이터 및 기타 어플리케이션의 요구사항들을 활용할 수 있다는 점에서 유연하다는 것이다. 그러나 문제가 있다. (수식 1)은 유저와 아이템 간 상호작용을 내포하기는 하지만, 실제 현실적으로는 유저 또는 아이템과 관련한 평점이 일관적이지 않을 수 있다. 같은 대상을 평가하더라도 어떤 사람은 후하게, 어떤 사람은 박하게 평가할 수 있기 때문이다. 이러한 것을 bias(또는 intercepts)라고 부른다.

이러한 이유로 (수식 1)을 진짜 평점이라고 여기는 것은 무리가 따른다. 즉, (수식 1)과 더불어 bias까지 고려해주어야 하는 것이다.

💡 (수식 6) $b_{ui}=\mu + b_i + b_u$

(수식 6)을 살펴보자. 평점 $r_{ui}$의 bias는 $b_{ui}$로 표기한다. 전체 평점의 평균은 $\mu$로, $b_{u}$와 $b_{i}$는 각각 유저와 아이템의 평균으로부터 얻어진 편차로 볼 수 있다.

복잡하니, 예를 들어보자. Joe라는 유저가 영화 타이타닉에 어떤 평점을 주었는지 예측하고 싶다고 해보자. 존재하는 모든 영화의 평균 평점이 3.7이라고 하면, 이것이 바로 $\mu$ 값이 된다. 이제 타이타닉의 평점을 보았더니, 평균보다 0.5 만큼 평점이 높았다고 하자. 그리고 Joe는 까다로운 사람이라서 평균 평점보다 0.3만큼 낮게 평점을 부여했다고 하자. 그러면 영화 타이타닉에 대한 Joe의 bias는 (3.7 + 0.5 - 0.3)으로 3.9가 된다.

💡 (수식 7) $\hat{r}_{ui} = \mu + b_i + b_u +q^T_ip_u$

이제는 (수식 7)과 같이 평점의 추정값이 더욱 구체화되었다. 즉, 실제 평균, 유저 bias, 아이템 bias, 그리고 유저-아이템의 상호작용을 내포하는 요인 벡터의 내적으로 구성된 것이다. 이로써 목적식을 재구성하면 아래와 같다.

💡 (수식 8) $\min\limits_{q^{\star},p^{\star}, b^{\star}}\sum\limits_{(u,i)\in \kappa}(r_{ui}-\mu-b_u-b_i-q_{i}^{T} p_{u})^{2}+\lambda(\lVert q_{i}\rVert^{2}+\lVert p_{u}\rVert^{2} + {b_u}^2 +{b_i}^2)$

06. Additional Input Sources

앞서 언급했듯 추천시스템은 초창기에 평점 정보를 얻기 어려우므로 cold start 문제가 존재할 수 있다. 이 경우, 유저에 대한 추가적인 정보를 제공해줌으로써 문제를 해결할 수 있는데, 이때 활용할 수 있는 것이 바로 implicit feedback 이다. implicit feedback은 유저가 직접적으로 explicit 한 평점을 부여하지 않더라도 유저의 행동을 통해서 파악할 수 있다. 예를 들어, 매장에서 고객이 무엇을 구매했는지 내역을 보면 해당 고객의 경향을 파악할 수 있을 것이다.

간단하게, 0과 1(boolean)로 implicit feedback을 받는다고 가정해보자. 이때 유저 u가 표한 implicit feedback을 표현한 아이템의 집합을 $N(u)$라고 표기한다고 해보자. 이제 아이템에 대해 implicit feedback을 표현했을 때 유저를 아래와 같이 정의할 수 있다.

💡 (수식 9) $\sum\limits_{i\in N(u)}x_i$

이때 새로운 요인(factor) 벡터는 $x_i∈ℝ^f$ 이다. 즉, 아이템 벡터와 동일한 $f$ 차원만큼 0과 1로 implicit feedback이 부여된 벡터이다. 그리고 이를 아래와 같이 정규화한다.

💡 (수식 10) ${|N(u)|}^{-0.5}\sum\limits_{i\in N(u)}x_i$

또 하나 사용할 수 있는 정보는 인구통계학 정보와 같이 이미 알려져있는 유저의 속성 정보이다. 이 또한 위와 같이 간단하게 0과 1의 boolean 속성으로 표현할 수 있다고 한다면, 유저 u에 대해 성별, 연령대, 우편번호, 연봉 등으로 $A(u)$라는 집합을 정의할 수 있겠다. 마찬가지로 이에 대한 새로운 요인 벡터 $y_a∈ℝ^f$를 통해서 아래와 같이 유저를 표현할 수 있다.

💡 (수식 11) $\sum\limits_{i\in A(u)}y_a$

위의 정보들을 종합하여 matrix factorization 모델을 더욱 풍부하게 표현할 수 있다.

💡 (수식 12) $\hat{r}{ui} = \mu + b_i + b_u +q^T_i \left[ p_u + |N(u)|^{-0.5}\sum\limits{i\in N(u)}x_i + \sum\limits_{i\in A(u)}y_a \right]$

07. Temporal Dynamics

지금까지는 평점 정보 등 모든 정보가 정적으로 정해져있다는 가정 하에서 계산을 하였지만, 실제로는 제품에 대한 인지도, 인기도 등이 수시로 변하며, 사용자의 선호도 또한 바뀐다. 그러므로 추천시스템이 시시각각 변하는 정보들 또한 반영할 수 있어야 한다.

matrix factorization 기법은 그 자체로 시시각각 변하는 선호도에 대해서 정확도를 높이기에 적합하다. 위 수식들에서와 같이 평점에 대한 추정값을 여러 term으로 쪼개는 방식 덕에 시시각각 변하는 정보들 또한 쉽게 표현할 수 있다. 구체적으로, 아이템 bias ($b_i(t)$), 유저 bias($b_u(t)$), 유저 선호도($p_u(t)$)가 시시각각 달라지는 term이라 할 수 있다.

이처럼 시간에 따라 변하는 term으로 평점에 대한 추정 값을 재구성해보면 아래와 같이 표현할 수 있다.

💡 (수식 13) $\hat{r}_{ui}(t) = \mu + b_i(t) + b_u(t) +q^T_ip_u(t)$

08. Inputs with Varying Confidence Levels

사실 모든 평점들이 동일한 가중치나 신뢰도를 가지지는 않는다. 예를 들어, 특정 아이템에 대해서 엄청나게 광고를 하면, 단기적으로 평점이 달라질 수 있다. 그리고 적대적인 고객이 있는 경우에 특정 아이템에 대해서 평점을 매우 박하게 줄수도 있다.

게다가 implicit feedback을 이용하는 시스템의 경우, 현재 유저의 행동을 바탕으로 아이템에 대한 명확한 선호도를 정량적으로 측정하기 어렵기도 하다. ‘이 아이템을 좋아할 것 같…다.?’와 같은 대략적인 정보만 알 수 있을 것이다. 이 경우, 신뢰 점수(confidence score)를 도입하는 것이 효과적일 것이다. 예를 들어, 해당 유저가 얼마나 자주 그 아이템을 구매하였는지와 같이 행동의 빈도를 기반으로한 수치들을 토대로 신뢰도를 구하여 활용할 수 있다. 한번만 있었던 행동은 별 의미가 없겠으나, 반복적으로 일어난 일들에 대해서는 유저의 의도가 반영되어 있을 수 있기 때문이다.

matrix factorization 모델은 이러한 신뢰도를 표현하기에도 적합하다. 더욱 의미 있는 사건에 대해서 많은 가중치를 주면 되기 때문이다. 이러한 평점 $r_{ui}$에 대한 신뢰도를 $c_{ui}$라고 표기한다면, 아래와 같은 수식으로 목적식을 표현함으로써 신뢰도를 반영할 수 있다.

💡 (수식 14) $\min\limits_{q^{\star},p^{\star}, b^{\star}}\sum\limits_{(u,i)\in \kappa}c_{ui}(r_{ui}-\mu-b_u-b_i-q_{i}^{T} p_{u})^{2}+\lambda(\lVert q_{i}\rVert^{2}+\lVert p_{u}\rVert^{2} + {b_u}^2 +{b_i}^2)$