이 포스트는 개인적으로 공부한 내용을 정리하고 필요한 분들에게 지식을 공유하기 위해 작성되었습니다.
지적하실 내용이 있다면, 언제든 댓글 또는 메일로 알려주시기를 바랍니다.
본 포스트 내용은
Stanford CS224w와 Query2Box 논문을 정리하였습니다.
들어가기에 앞서
추론(reasoning) 이란 ?
추론(reasoning)이란, 온톨로지(i.e., knowledge base) 상에 명확하게 표현되어 있지 않은 사실(지식)에 대해 기계가 논리적(i.e., 의미론적(semantic))으로 추론하는 것을 의미한다.
온톨로지에서 지식은 논리학을 다루는데, 논리학은 원론적으로 명제논리(propositional logic)를 기반으로 한다. 즉, 논리적 연결사(logical connective)에 의해 참 혹은 거짓을 따질 수 있는 문제에 관한 논리를 다루는 것이다. 이러한 명제논리의 기초 위에 술어논리(predicate logic)가 성립한다. 술어논리는 ‘주어’와 ‘술어’로 구성된 문장에서 ‘주어’에 한정기호를 사용하는 방식으로, 대표적으로는 1차 논리(First-order Logic(FOL))가 있다. 온톨로지 기반의 AI는 1차 논리 계산에 근거하여 정답을 내놓는다.
우리는 주어진 상황에 대한 지식을 가지고 새로운 사실을 유도하는 데 익숙해 있다. 실제 우리가 알고 있는 모든 과학적 사실들이 일정한 추론의 틀에서 비롯되었다고 하여도 과언이 아니다. 즉, 추론(reasoning, inference, argument)이란, 이미 알고 있는 명제를 기초로 하여 새로운 명제를 유도하는 과정으로 전제(premise)와 결론(conclusion) 간의 논리적 관계를 다룬다.
본 논문은 임베딩 공간에서 벡터로 표현된 KG를 어떻게 추론(reasoning)하는지에 대해서 다룬다. 특히, conjunction(∧), disjunction(∨), existential quantifier(∃) 등으로 복잡하게 표현되는 multi-hop 질의에 대해서도 임베딩 공간에서 결과를 추론할 수 있는 방법론을 제시한다.
질의의 유형별 추론
KG에서 어떠한 사실을 추론하기 위한 질의는 아래와 같이 나눌 수 있다.
- One-hop Queries
- (e.g.) Where did Hinton graduate?
- Path Queries(Multi-hop Queries)
- (e.g.) Where did Truing Award winners graduate?
- Conjunctive Queries
- (e.g.) Where did Canadians with Turing Award graduate?
- 기타 (Existential Positive First-order(EPFO) Queries)
- (e.g.) Where did Canadians with Turing Award or Nobel Graduate?
One-hop 질의
간단한 One-hop 질의에 대해 임베딩을 활용하여 추론한다면, KG completion의 link prediction 문제를 푸는 방식으로 해결할 수 있다. link prediction은 (h, r, ?) 혹은 (?, r, t)가 주어졌을 때, 누락된 ?를 알아내는 문제이므로 one-hop 질의에 대해 추론할 수 있다.
Path 질의
Path 질의는 one-hop 질의에서 여러 relation이 추가되어 정답을 찾아가는 경로가 길어진 형태이다. 즉, “Where did Turing Award winners graduate?” 라는 질의에 답을 찾기 위해서는 아래와 같이 “Turing Award”라는 anchor node로부터 “win”과 “graduate” relation을 순회하며 최종적인 정답을 추론해야 한다.
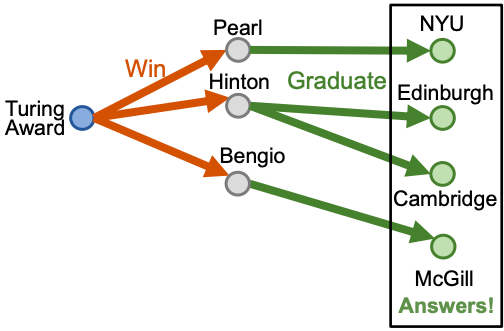
그러나 KG는 인간이 입력한 데이터로 구성된 그래프이기 때문에 본연적으로 incomplete하다. 따라서 missing edge에 대한 순회가 제한되기 때문에 추론 결과 또한 제한될 수밖에 없다. 그렇다면 KG completion을 미리 수행하여 완벽한 KG에 대해서 path 질의에 대해 추론하면 되지 않는가? 이 경우, 그래프는 매우 복잡해지므로 그래프를 순회하기 위한 시간 복잡도가 intractable 할 정도로 늘어나게 된다.
이처럼, 불완전한 KG에서 path 질의의 정답을 추론하기 위해서는 임베딩을 활용했던 one-hop 추론 방법을 multi-hop에 응용함으로써 가능하다. 이는, anchor node로부터 이어지는 relation들을 질의 q로 정의하고, q를 임베딩하는 방식이다. 이때 질의 벡터 q는 entity들의 수와 상관 없이 anchor node 및 relation 벡터들의 단순한 합으로 임베딩한다.
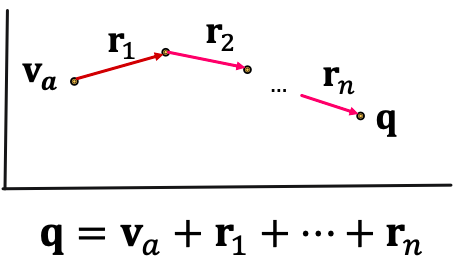
이후 과정은 TransE와 유사하다. TransE에서 h + r = t 가 됨을 이용했던 것처럼, 질의 벡터 q는 원하는 추론 결과 근처에 존재하게 될것이므로, q에 대해 nearest neighbor search를 한다면 추론 결과 노드들을 구할 수 있다. 이는 직접 그래프를 순회하지 않고 approximation으로 추론을 하는 방법으로 시간 복잡도가 O(V)로 적다.
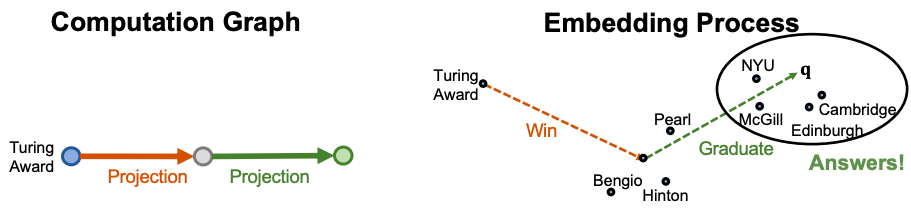
Conjunctive 질의
conjunction(∧)으로 이루어진 복잡한 질의의 경우, 어떻게 KG에서 추론할 수 있을까? “Where did Canadians with Turing Award graduate?” 질의를 예로 들어보자.
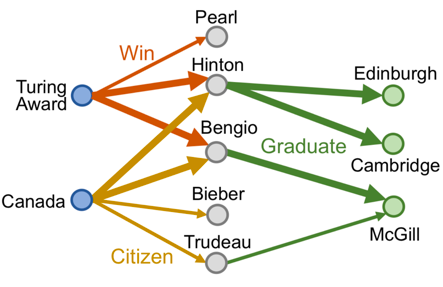
만약, KG가 complete 하다면, 위와 같이 순회를 함으로써 쉽게 답을 구할 수 있겠으나, 언제나 그렇듯 KG는 항상 incomplete하다. 따라서 이 또한 path 질의에서와 같이 질의 자체를 벡터로 임베딩함으로써 정답을 approximation 하는 방법으로 접근해 볼 수 있다.
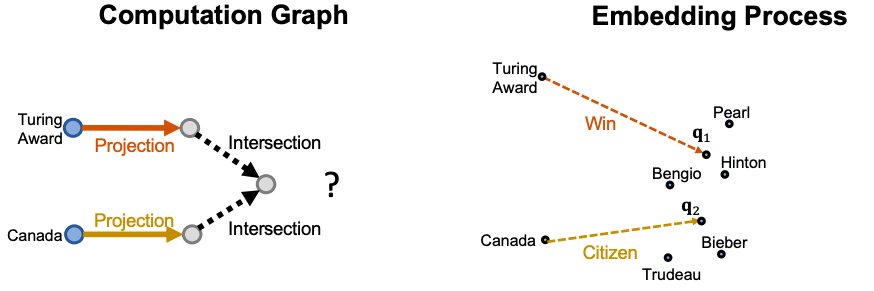
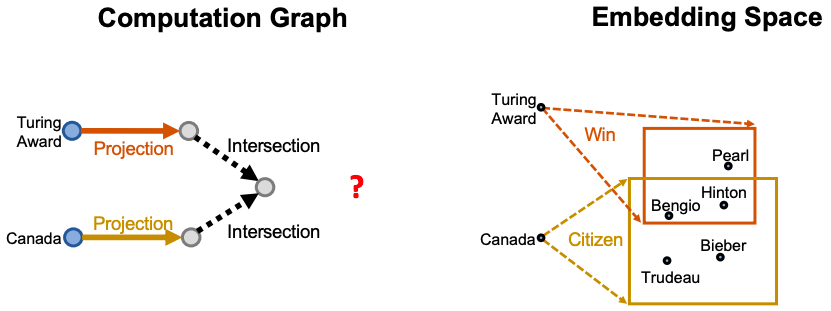
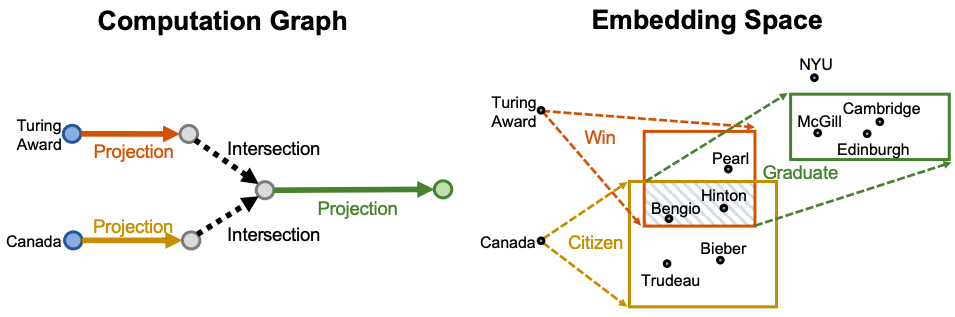
위와 같이 anchor node들인 “Turing Award”와 “Canada”에서 각각의 질의 벡터를 통해 q1과 q2 지점으로 projection을 완료했다. 즉, 두 지점 사이의 ‘어떠한 지점’(i.e., intersection)이 바로 두 질의의 공통된 부분에 해당되므로 해당 지점의 근처가 논리적으로 질의들의 conjunction을 구현한 부분이 된다. 그렇다면 ‘어떠한 지점’은 어떻게 구할 수 있을까?
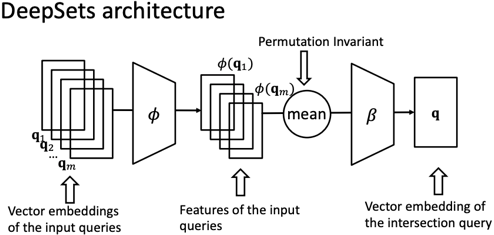
벡터들의 intersection은 아래와 같이 DeepSets으로 구현한 neural intersection operator J를 통해 구할 수 있다. 즉, DeepSets 모델에 인풋으로 질의 임베딩을 넣으면, 아웃풋으로 질의의 intersection 임베딩 벡터가 나오는 형태이다.
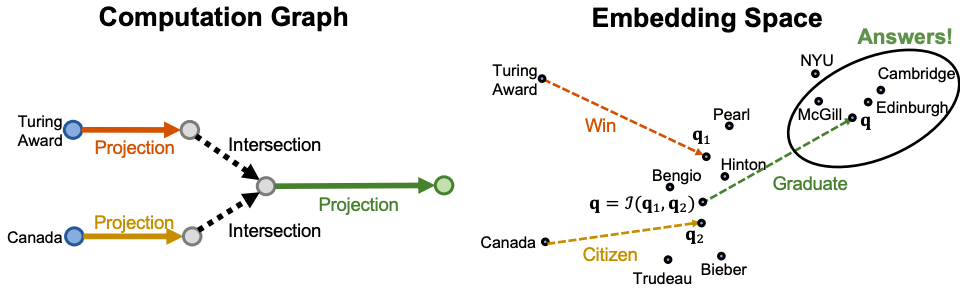
이처럼 intersection 임베딩 벡터로 ‘어떠한 지점’을 구하고 해당 지점에서 남은 경로마저 approximation 한 후, nearest neighbor search를 수행하면, conjunctive 질의에 대한 최종적인 추론이 가능하다.
Query2Box
Box Embedding
지금까지는 질의(i.e., 그래프 상에서의 relation)를 하나의 벡터로 임베딩하여 정답을 approximation하여 추론하였다. 그러나, Query2Box 논문은 질의를 기하학적인 box로 임베딩을 한다. box는 hyper-rectangle로 표현되며, box 형태의 질의 임베딩은 아래와 같이 정의된다.
(강의 자료 및 원 논문을 함께 정리하는 본 글은 원 논문과 약간의 notation 차이가 있다.)
이때 Center는 box의 중심 좌표를, Offset은 해당 축에서 box의 중점으로부터 모서리까지의 길이(즉, 너비(?))를 의미하고, 각각 d 차원의 벡터로 표현된다.
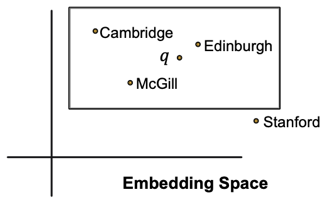
위와 같이 box 임베딩을 활용한다면, 질의가 임베딩 공간에 projection되는 부분이 ‘어떠한 지점’이 아닌 ‘어떠한 영역’으로 표현된다. 즉, 질의의 결과에 해당하는 entity들을 모두 포함하는 영역이 되는 것이다.
box 형태로 질의를 임베딩한다면, intersection 연산을 잠재 공간 상에서 기하학적으로 수행할 수 있다. 단순히 질의 box들이 겹치는 부분들이 intersection(i.e., conjunction)인 것이다. 매우 직관적이라는 장점이라고 할 수 있다.
box 임베딩을 학습하기 위한 파라미터는 다음과 같다.
1) entity embeddings : d 차원
- 각각의 entity는 offset이 0인 box로 본다. 즉, box 형태가 사라져 점으로만 표현되는 느낌이다.
2) relation(i.e., query) embeddings : 2d 차원
최초의 entity에 대한 box는 (v 벡터, 0 벡터)로, d차원의 v벡터를 중점으로 크기가 0인 box로 볼 수 있다.
각각의 relation(질의)은 box 형태를 input으로 받아 새로운 box를 output으로 낸다.
3) intersection operator φ and β
intersection을 수행하는 DeepSets 모델에 존재하는 파라미터로, 그래프의 크기가 어떠한지와 관계없이 φ와 β의 파라미터 수는 독립적이다.
벡터를 대상으로 intersection을 수행하지 않고, box를 대상으로 intersection을 수행한다.
box 임베딩에 대해서 더욱 구체적으로 살펴보자.
Geometric Projection Operator
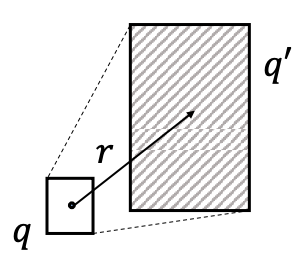
geometric projection은 질의 벡터 r(i.e., relation)을 통해 기존의 box q(c.f., 단일 entity 또한 크기 0인 box)가 공간상에서 새로운 box q’으로, 기하학적으로 projection되는 과정을 말한다. 이를 수식으로 표현하면 다음과 같다.
(강의 자료 및 원 논문을 함께 정리하는 본 글은 원 논문과 약간의 notation 차이가 있다.)
$Offset(\mathbf{q'})=Offset(\mathbf{q})+Offset(\mathbf{r})$
이 때 offset은 항상 0보다 크거나 같으므로, 질의 벡터 r에 의해 새로이 projection되는 box는 항상 기존의 box의 크기와 같거나 커지게 된다. 생각해보면, box가 계속해서 커져야 더 많은 entity들을 포함시킬 수 있으니 당연한 것이다.
질의 벡터로 새로이 box를 projection하면, 위와 같이 box가 겹치는 intersection이 생길테고, 그것이 바로 논리적으로는 conjunction에 해당하는 것이다. 그렇다면, 공간 상에 존재하는 이 intersection을 어떻게 집어낼 것인가?
Geometric Intersection Operator
geometric intersection operator는 이러한 box들의 intersection을 모델링한다.
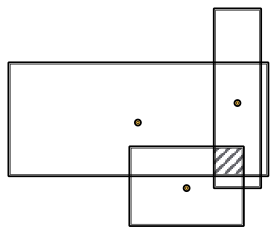
위 그림에서와 같이, box들이 겹치는 영역에 대해 intersection(i.e., conjunction)이 구현된 새로운 box로 정의하기 위해서는 box의 정의에 따라 새로운 box에 대한 center와 offset을 구해야 한다.
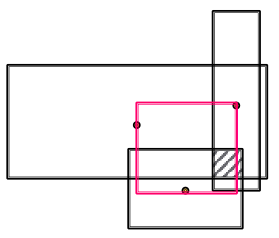
1) intersection box 영역에서의 center
새로운 box의 center의 경우, 위 그림과 같이 intersection을 구하고자 하는 box들의 center들을 이어 만든 빨간색 영역 안에 존재해야 한다. Query2Box 논문에서는 해당 영역에서 새로운 box의 center를 구하기 위해서 기존 box들의 center들을 대상으로 self-attention 메커니즘을 적용하여 계산한다. 이를 수식으로 나타내면 아래와 같다.
(강의 자료 및 원 논문을 함께 정리하는 본 글은 원 논문과 약간의 notation 차이가 있다.)
이 때, $MLP(\cdot)$는 multi layer perceptron을, $w_i$는 attention weight를 의미한다. (c.f., 원 논문에서는 attention weight를 구하기 위해서 $\mathbb{R^d}$차원인 $Center(\mathbf{q_i})$ 대신 $\mathbb{R^{2d}}$차원인 $\mathbf{q_i}$ 를 $MLP$의 input으로 간주한다. 이때의 $MLP$는 $\mathbb{R^{2d}}\rightarrow\mathbb{R^d}$로의 함수이다.)
2) intersection box 영역에서의 offset
새로운 box의 offset 또한 구해보자. intersection box의 offset은 반드시 intersection을 수행하려는 input box들의 offset보다 작아야 한다. 그 이유는, 앞서 질의 벡터를 활용한 projection으로 box를 키움으로써 많은 후보 entity들을 box 안에 포함시켰으니, 그 중에서 conjunction에 해당하는 entity들만 추려내야 하기 때문이다. offset을 구하기 위한 과정은 약간 더 복잡한데, 그 과정은 아래와 같다.
(강의 자료 및 원 논문을 함께 정리하는 본 글은 원 논문과 약간의 notation 차이가 있다.)
$where \ \sigma(\cdot) \ is \ the \ sigmoid \ function $
이때 $DeepSets({\mathbf{x_1, \ldots, x_N}})=MLP((1/N) \ \cdot \ \sum_{i=1}^N MLP(\mathbf{x_i}))$로 정의할 수 있는데, 즉 input box들의 offset에 대한 평균적인 representation을 $MLP$로써 뽑아내는 기능을 수행한다. 이는 sigmoid $\sigma(\cdot)$ 함수를 거쳐서 (0, 1)의 output 범위를 가지게 되며 input box의 offset 중 최솟값과 곱해지는데, 이러한 과정에서 intersection box의 offset은 반드시 input box의 offset보다 작은 값을 가질 수 있게 된다.
이 모든 과정을 거쳐서 구한 intersection 영역의 center와 offset은 아래와 같이 임베딩 공간에서 conjunction의 기능을 수행하게 된다.
Entity-to-box Distance
그렇다면 projection을 통해서 box $\mathsf{q}$를 구했을 때, $\mathsf{q}$와 실제 우리가 추론하고자 했던 entity들은 공간 상에서 얼마나 가까운 곳에 존재할까? Query2Box는 query box $\mathsf{q}\in\mathbb{R^{2d}}$와 entity vector $\mathsf{v}\in\mathbb{R^d}$ 가 주어졌을 때, 아래와 같이 그 거리를 정의한다.
(강의 자료 및 원 논문을 함께 정리하는 본 글은 원 논문과 약간의 notation 차이가 있다.)
$where \\ \mathsf{q_{max}}=Center(\mathsf{q})+Offset(\mathsf{q}) \in\mathbb{R^d} , \ \ \mathsf{q_{min}}=Center(\mathsf{q})-Offset(\mathsf{q}) \in\mathbb{R^d}$
$and \ \ 0\lt\alpha\lt1 \ is \ a \ fixed \ sclar$
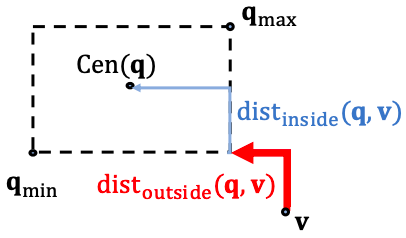
이때 $dist_{outside}$는 box 바깥에 위치한 entity 벡터의 위치부터 box의 가장 가까운 모서리까지의 거리를, $dist_{inside}$는 box 내부에 위치한 entity 벡터의 위치부터 box의 중점까지의 거리를 의미하며 아래와 같이 표현된다.
(강의 자료 및 원 논문을 함께 정리하는 본 글은 원 논문과 약간의 notation 차이가 있다.)
$dist_{inside}(\mathsf{q,v})= \lVert Center(\mathsf{q})-Min(\mathsf{q_{max}}, Max\mathsf{(q_{min}, v})) \rVert_1$
독특한 점은, 거리를 구하는 식 $dist_{box}(\mathsf{q, v})=dist_{outside}(\mathsf{q, v})+\alpha \ \cdot \ dist_{inside}(\mathsf{q, v})$에서 $dist_{inside}$ 앞에 $\alpha$가 붙는다는 것이다. 왜일까? 이는 entity 벡터가 box 안에 존재할 때는 query box의 중점과 “충분히” 가깝기 때문에 그 거리에는 downweight를 가하는 것이다. 즉, 이때의 $dist_{outside}$는 0의 값을 가지며, $\alpha$의 값만큼 scale된 $dist_{inside}$의 값으로만 거리에 대한 값이 결정된다.
Training Objective
질의에 대해서 추론하고자 하는 사실(i.e., entity 벡터)과 질의에 대한 projection인 box 사이의 거리인 $dist_{box}$를 계산할 수 있게 되었다. 그렇다면 이제부터는 질의와 그에 대한 정답이 학습 데이터셋으로 존재할 때, 목적함수인 loss function을 정의함으로써 Query2Box를 학습할 수 있다. loss function은 다음과 같다.
(강의 자료 및 원 논문을 함께 정리하는 본 글은 원 논문과 약간의 notation 차이가 있다.)
$where \ \gamma \ represents \ a \ fixed \ scalar \ margin,$
$v \in \lbrack q \rbrack \ is \ a \ positive\ entity,$
$v_j'\notin \lbrack q \rbrack \ is\ the\ i-th\ negative\ entity$
$and\ k\ is\ the\ number\ of\ negative\ entities.$
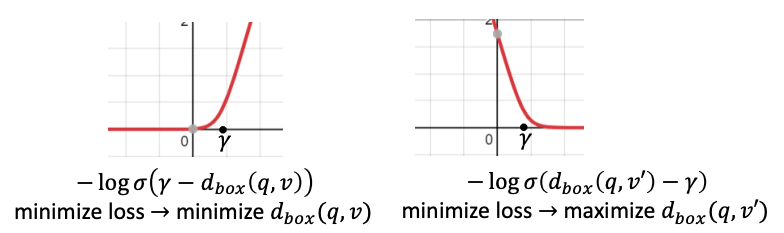
위의 그림을 보면(수식은 약간 다르지만 결국 같은 이야기다.), (왼쪽)질의에 대해 정확한 정답에 해당하는 벡터 $v$는 query box와의 거리가 가까울수록 box에 포함될 수 있으므로 $dist_{box}$를 최소화하는 쪽으로 최적화된다. 반면에, (오른쪽)질의에 대한 오답으로 형성된 벡터 $v’$은 query box와 거리가 멀수록 box에 포함되지 않을 수 있으므로 $dist_{box}$를 최대화 하는 방향으로 최적화된다.
또한 $\gamma$는 TransE에서와 같이 margin을 의미한다. 그림의 왼쪽의 경우, $\gamma$보다 작은 영역은 loss가 매우 작으므로, $\gamma$보다 작은 영역에서 loss 값이 형성되는 것을 penalize 하여 loss를 부풀린다. 반대로, 오른쪽의 경우, $\gamma$보다 큰 영역이 매우 작은 loss 값을 가지므로, 해당 영역부터 penalize 하여 loss를 부풀린다.
Tractable Handling Of Disjunction Using Disjunctive Normal Form(DNF)
지금까지는 path 질의, conjunctive 질의를 효과적으로 box를 이용하여 추론하였다. 그러나 우리가 다루어야 할 질의들은 이 외에도 disjunction(∨), existential quantifier(∃) 등 더욱 복잡한 논리가 표현되어 있을 수 있다. 이러한 질의를 Existential Positive First-order(EPFO) 질의라 부른다.
EPFO 질의처럼 disjunction이 포함된 질의를 처리할 수 있는 가장 직관적인 방법은 기하학적인 box에 대해 union 연산을 수행하는 것이다. 즉, entity set ${S_1, S_2, \cdots, S_n}$이 주어졌을 때 $\cup_{i=1}^nS_i$를 수행하는 것이다. 하지만, 임베딩 공간 상에서 box(혹은 entity)는 어디에나 존재할 수 있다. 따라서 현실적으로 box에 대해서 union을 취하는 연산은 간단한 box의 형태가 아닐 것이다. 즉, box에 대한 union 연산은 닫혀있지 않다.
이러한 문제를 다루기 위해서, Query2Box는 EPFO 질의를 논리적으로 동치 관계인 Disjunctive Normal Form(DNF)으로 변환할 것을 제안한다.
여기서 잠깐! DNF의 정의를 잠깐만 간단하게 짚고 가보자. 명제논리에서 “atomic sentence”란 참 또는 거짓으로 표현할 수 있는 단 하나의 명제로 구성되어 있는 최소 단위 문장을 의미한다. 이때 atomic sentence를 “literal”이라고 부르는데, not을 의미하는 negation(¬) 기호가 없는 경우를 positive literal, negation 기호가 있는 경우를 negative literal이라 부른다. DNF란, “(literal들의 conjunction들)에 대한 disjunction”으로 이루어진 형태를 뜻하며 그 예는 아래와 같다.
- ${\displaystyle (A\land \neg B\land \neg C)\lor (\neg D\land E\land F)}$
- ${\displaystyle (A\land B)\lor C}$
- $A\land B$
- ${\displaystyle A}$
즉, Query2Box의 제안대로 1차 논리(First-order Logic(FOL))를 DNF로 전환하는 것은 결국 conjunction 질의들에 대하여 마지막 과정에서 단 한번의 disjunction, 즉, 단 한번의 union 연산만을 수행하는 것을 의미한다.
Transformation to DNF
모든 1차 논리는 논리적으로 동치인 DNF 형태로 변환할 수 있다(Davey & Priestley, 2002). Query2Box 논문에서는 아래와 같이 computation graph의 space 상에서 직접 모든 union 연산을 최후의 step으로 옮김으로써 DNF를 구현하였다.

다시 말하자면, conjunctive query들을 먼저 임베딩 한 후, 이를 마지막 단계에서 aggregate 하는 방식을 쓴다는 것이 핵심이다.
Aggregation
앞서 정의했듯이 conjunctive 질의를 box $\mathbf{q_i}$라고 표현한다면, DNF 형태로 수식을 표현하자면 아래와 같다.
만약 우리가 추론하고자 하는 정답 $v$가 conjunctive 질의 $\mathbf{q_i}$ 중 하나의 정답이라면, 이는 곧 논리적으로 $\mathbf{q}$의 정답이라고 볼 수 있다. 즉, $v$가 conjunctive 질의 $\mathbf{q_i}$ 중 어느 하나와 임베딩 공간 상에서 가까이 위치한다면, $v$는 궁극적으로 $\mathbf{q}$와 가깝다. 따라서 DNF를 적용할 경우, 목적식인 거리 함수는 다음과 같이 정의된다.