이 포스트는 개인적으로 공부한 내용을 정리하고 필요한 분들에게 지식을 공유하기 위해 작성되었습니다.
지적하실 내용이 있다면, 언제든 댓글 또는 메일로 알려주시기를 바랍니다.

💡 오일러 공식 : $ e^{ix}=\cos{x} + i\sin{x} $

00. Intro

오일러 공식은 세상에서 가장 아름다운 수학 공식으로 알려져있으며, 천재 수학자 오일러에 의해 정의되었음
오일러 공식은 지수함수와 삼각함수에 대한 관계를 나타내며, 전자공학, 진동학, 제어공학 등에서 매우 중요한 수학적 토대가 되었음
특히, 필자는 음성 AI를 공부하며 음성 신호를 시간 도메인에서 주파수 도메인으로 변환하는 푸리에 변환을 공부하며 오일러 공식을 접하게 되었고, 이를 아래와 같이 정리하고자 함

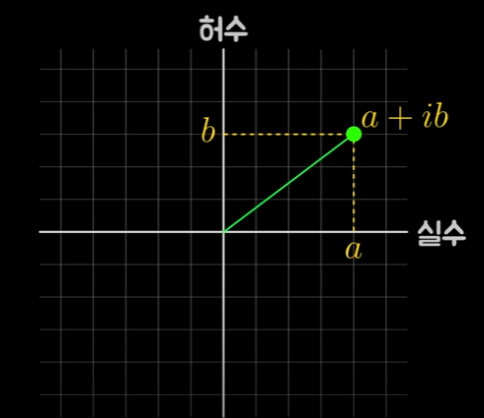
fig01

복소평면 상에서 실수 측 좌표 $a$와 허수측 좌표 $b$ 위치에 있는 점은 $a+ib$라는 복소수에 대응됨

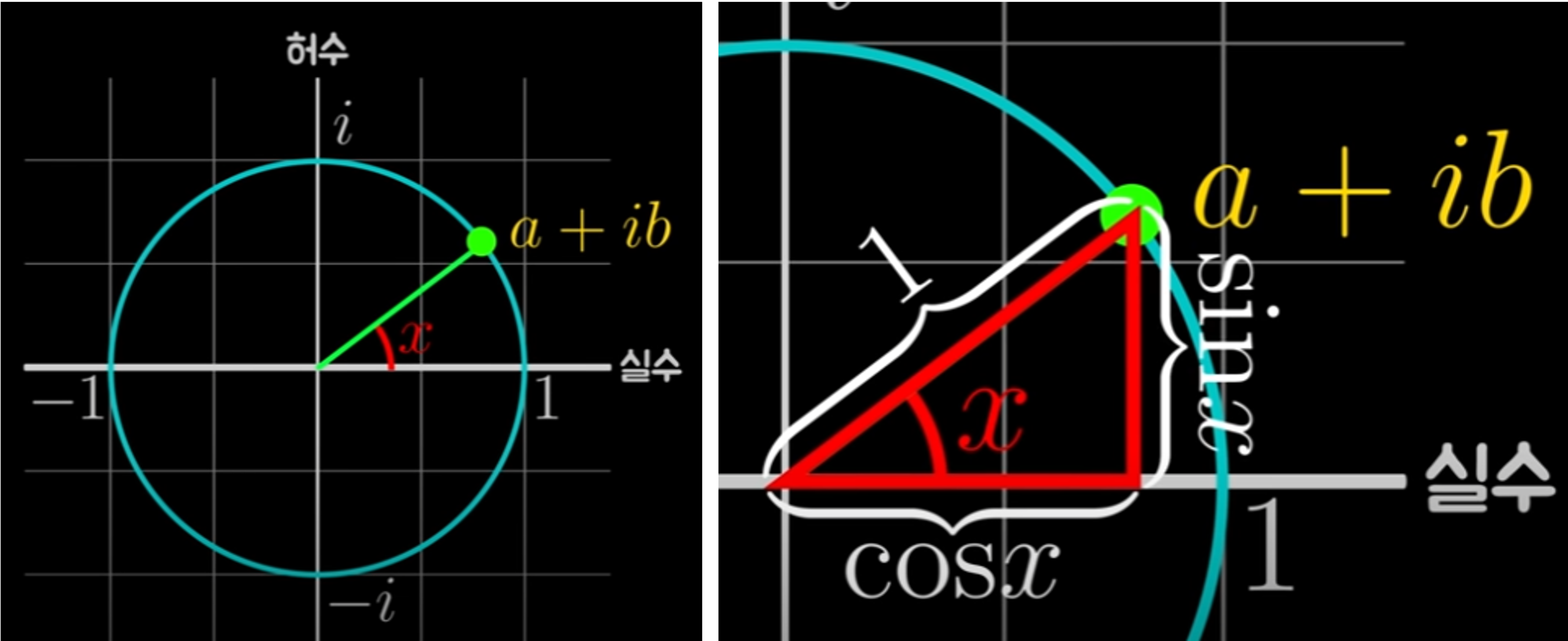
fig02

복소평면 상에서 반지름이 1인 단위원을 그려놓고, 실수 측과의 각도, 즉, 편각이 $x$인 위치에 있는 이 복소수는 실수 부분과 허수 부분이 각각 $\cos{x}$와 $i\sin{x}$에 대응되어 $\cos{x}+i\sin{x}$에 대응됨
그리고 이 수는 각도 $x$에 따라 달라지는 일종의 함수이므로, $f(x)=\cos{x}+i\sin{x}$라고 표현할 수 있음

01. f(x)의 성질

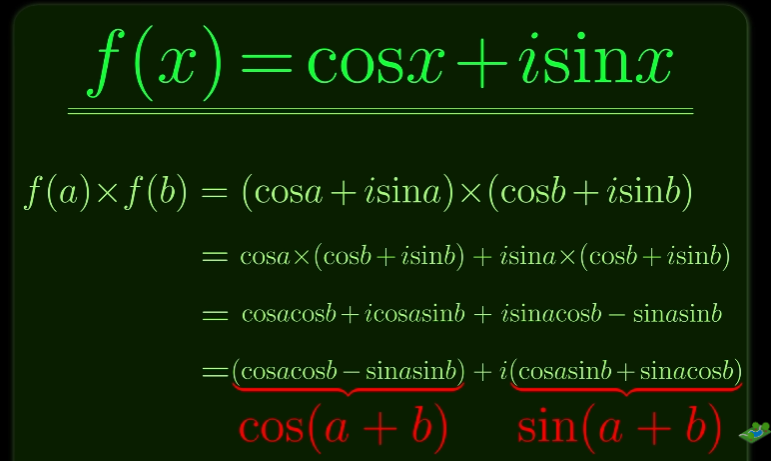
fig03

제1차 성질

$f(a) \times f(b)$

$= (\cos{a}+i\sin{a}) \times (\cos{b}+i\sin{b})$

$= \cos{a} \times (\cos{b}+i\sin{b}) + i\sin{a} \times (\cos{b}+i\sin{b})$

$=\cos{a}\cos{b}+i\cos{a}\sin{b} + i\sin{a}\cos{b}+i^2\sin{a}\sin{b}$

$=\cos{a}\cos{b}+i\cos{a}\sin{b} + i\sin{a}\cos{b}-\sin{a}\sin{b}$

$=(\cos{a}\cos{b}-\sin{a}\sin{b})+i(\cos{a}\sin{b}+\sin{a}\cos{b})$

$=\cos{(a+b)}+i\sin{(a+b)}$

(공식 참고) 삼각함수의 곱을 합과 차로 표현

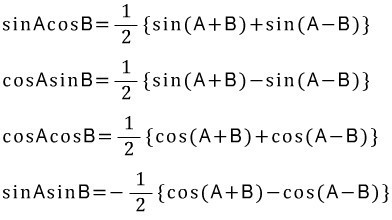
formulas

$= f(a+b)$ [제1차 성질]

제2차 성질

$f(x) \times f(x) = f(x+x)$

${f(x)}^2 = f(2x)$ [제2차 성질]

제3차 성질

$\cfrac{1}{f(x)}=\cfrac{1}{f(x)} \times 1$

$= \cfrac{1}{f(x)} \times \cfrac{f(-x)}{f(-x)} = \cfrac{f(-x)}{f(x) \times f(-x)}$

이때, 분모에 [제1차 성질]을 적용하면,

$f(x) \times f(-x) = f(x-x) = f(0) = \cos{(0)}+i\sin{(0)}$ 이고,

$\cos{(0)}=1$ 이고, $\sin{(0)}=0$ 이므로, $f(0)=1$이 됨

따라서, 분모가 1이 되므로 아래의 식이 유도됨

$\cfrac{1}{f(x)} = f(-x)$ [제3차 성질]

제4차 성질

[제3차 성질]의 유도 과정에서 도출한 $f(0)=1$ [제4차 성질]

제5차 성질

$f\prime(x)=(\cos{x}+i\sin{x})\prime$

$=(\cos{x})\prime + (i\sin{x})\prime$ … 더해져 있는 것의 미분은 앞 뒤를 각각 미분하는 것과 동일함

$=-\sin{x}+i\cos{x}$

$=i^2\sin{x}+i\cos{x}$

$=i(\cos{x}+i\sin{x})$

$=if(x)$ [제5차 성질]

중요한 발견!

위에서 정리한 복소평면 상에서의 함수 $f(x)$의 성질은 자연상수 $e$를 밑으로 하는 지수함수 $e^x$와 그 성질이 매우 비슷함
- $f(a) \times f(b) = f(a+b)$ [제1차 성질]
  - $e^a \times e^b=e^{a+b}$
- ${f(x)}^2 = f(2x)$ [제2차 성질]
  - ${e^x}^2=e^{2x}$
- $\cfrac{1}{f(x)} = f(-x)$ [제3차 성질]
  - $\cfrac{1}{e^x}=e^{-x}$
- $f(0)=1$ [제4차 성질]
  - $e^0=1$
- $f\prime(x)=if(x)$ [제5차 성질]
특히, $e^{ix}$의 성질은 [제5차 성질]까지 모두 만족함
- $f(a) \times f(b) = f(a+b)$ [제1차 성질]
  - $e^{ia} \times e^{ib}=e^{i(a+b)}$
- ${f(x)}^2 = f(2x)$ [제2차 성질]
  - ${e^{ix}}^2=e^{i2x}$
- $\cfrac{1}{f(x)} = f(-x)$ [제3차 성질]
  - $\cfrac{1}{e^{ix}}=e^{-ix}$
- $f(0)=1$ [제4차 성질]
  - $e^{i \times 0}=1$
- $f\prime(x)=if(x)$ [제5차 성질]
  - $(e^{ix})\prime = ie^{ix}$

02. 오일러 공식의 정리

지수함수 $e^{ix}$는 복소평면 단위 원 상의 함수 $\cos{x} + i\sin{x}$와 동일함
따라서 지수함수 $e^{ix}$는 주기함수의 성질이 있음

오일러 등식

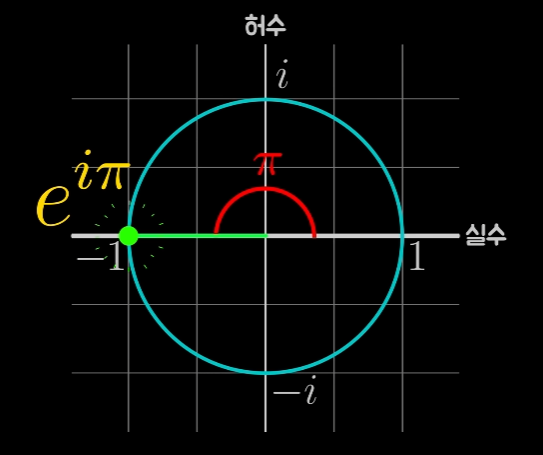
fig04

오일러 등식
- $e^{i \pi}=-1$ 이므로, $e^{i \pi}+1=0$이 성립함
해석
- $e$는 미적분을 대표하는 수
- $i$는 복소수를 대표하는 수
- $\pi$는 기하를 대표함
- 0과 1은 어떤 정보를 표현하는 최소 단위에 해당함
⇒ 이렇게 중요하고 대표적인 숫자들이 단지 $+$와 $=$만으로 표현된다는 것은 엄청난 사건임

03. 참고

[1] DMT PARK 님의 강의
[2] Wikipedia