이 포스트는 개인적으로 공부한 내용을 정리하고 필요한 분들에게 지식을 공유하기 위해 작성되었습니다.
지적하실 내용이 있다면, 언제든 댓글 또는 메일로 알려주시기를 바랍니다.

본 포스트의 상당 내용은 인과추론의 데이터과학 강의를 정리한 것임을 밝힙니다.

00. 들어가며

필자가 인과추론을 공부하기 시작한 이유는 클라우드 인프라 자원의 장애 발생에 대한 근본 원인을 탐지하는 기술을 연구하기 위해서입니다. 관련된 선행 연구를 보았을때, 많은 경우에 인프라 자원에 대하여 인과그래프를 구축하고,이를 대상으로 BFS/DFS 탐색을 하든 나름의 랭킹 알고리즘을 활용하든 하여 장애를 탐지하는 방식을 쓰는 것을 확인했습니다. 또, 특정 연구들은 인과그래프를 구축하기 위해서 PC 알고리즘이라는 것을 활용하기도 했습니다. 이러한 연구들을 파악하기 위해서 기본적인 인과추론에 대한 이해가 필요했었고, 인과추론이라는 새로운 영역을 공부하게 됐습니다. 그리고 드디어 인과그래프를 구축하기 위해서 많은 선행 연구들이 사용했던, 그리고 선행 연구를 보며 가장 궁금했던 PC 알고리즘을 다루고자 합니다.

01. Causal Discovery

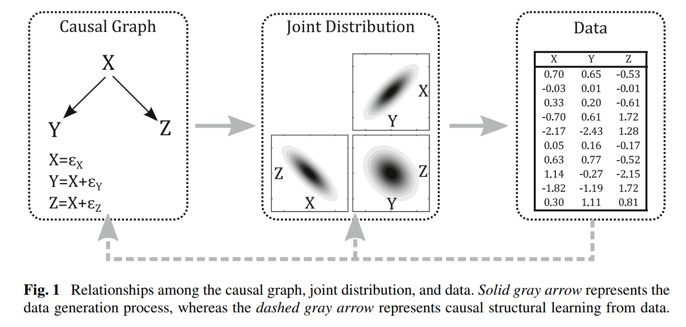
causal_structural_learning

지금까지 공부했던 Structural Causal Model은 모두 잘 정의되어 있는 인과그래프가 이미 존재한다는 것을 전제로 하고 있습니다. 위 그림을 보겠습니다. 잘 정의되어 있는 인과그래프는 Joint Distribution으로 표현될 수 있습니다. 그리고 이러한 그래프와 Joint Distribution을 따르는 데이터를 활용하면 인과관계의 효과를 추정할 수 있습니다. 이러한 방식이 지금까지 공부했던 Structural Causal Model 입니다.

그런데 현실에서는 인과그래프를 구축하기 어려운 경우가 많습니다. 우리는 신이 아니기 때문에, 어떤 변수가 다른 변수에 어떻게 영향을 주는지 명확히 알기 어려운 것이죠. 이러한 문제가 Structural Causal Model의 한계점이기도 합니다. 즉, 완벽한 그래프가 주어진다면, 이론적으로 완벽한 인과적 효과를 계산할 수 있는 방법이긴 하지만, ‘완벽한 그래프’가 구축되기 어려우며, 상당한 도메인 지식도 필요로 할 것입니다.

이러한 문제를 어느정도 완화해줄 수 있는 방법이 있는데, Causal Discovery가 그것입니다. 그림에서 점선으로 표시된 화살표를 보겠습니다. Structural Causal Model의 역방향으로 흐르고 있죠. Causal Discovery는 Structural Causal Model과 반대로, 데이터가 존재할 때, 해당 데이터를 분석하여 데이터 내 Joint Distribution을 파악하고, 파악한 내용들로 인과그래프를 직접 도출하는 방식입니다. 이처럼 데이터를 활용해서 역으로 인과그래프의 구조 자체를 도출하는 방식이기에 Structure Identification이라고도 불립니다.

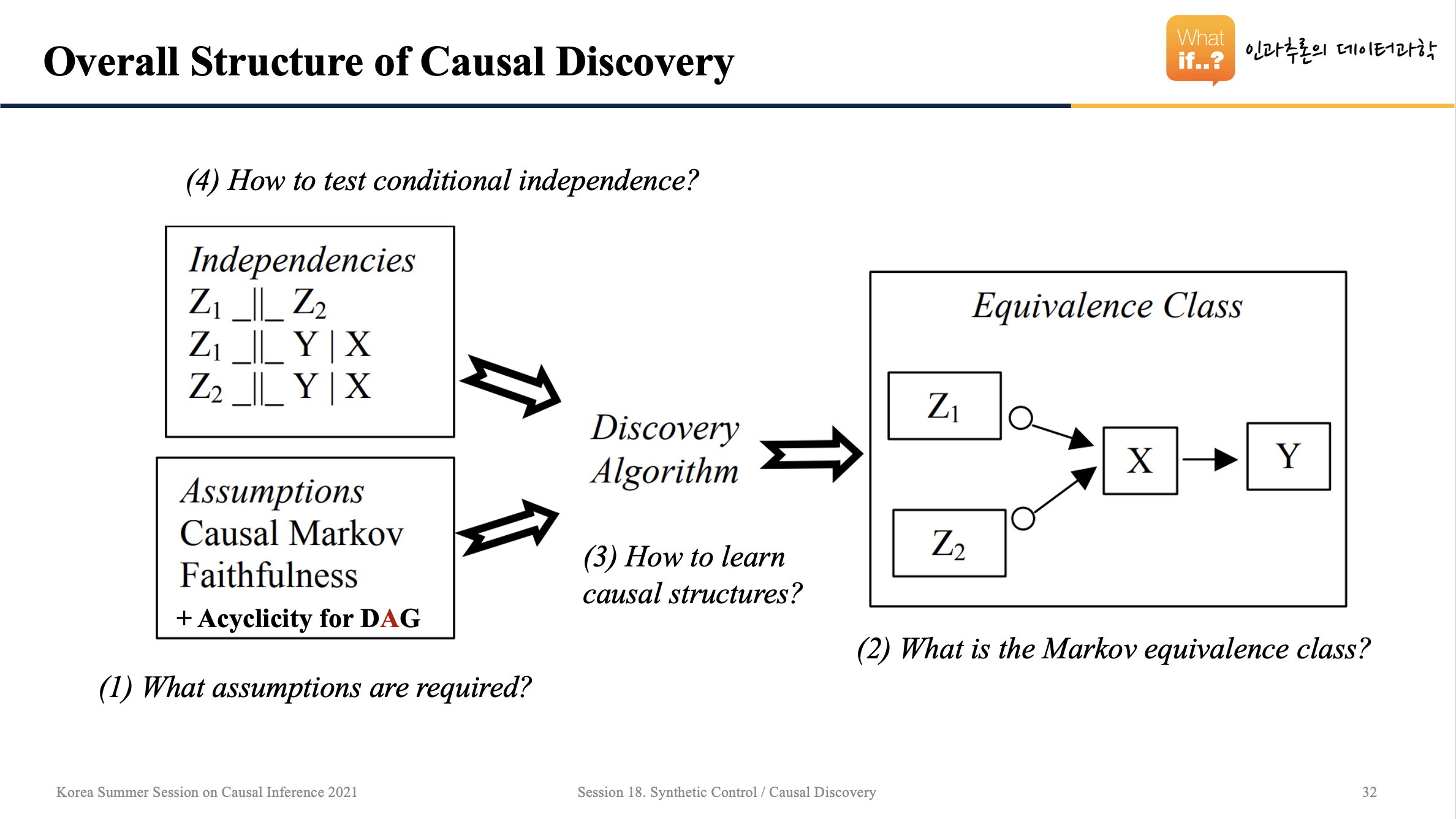
overall_structure_of_causal_discovery

위의 장표는 Causal Discovery의 전체적인 구조를 보여줍니다. 우선, 데이터 상에 존재하는 변수들 간의 Joint Distribution을 이용해서 변수들이 독립인지, 종속인지를 파악해야 합니다. 그리고 몇 가지의 가정들을 만족했다는 전제하에 Causal Discovery 알고리즘을 돌립니다. 그러면 Equivalence Class라고 부르는 인과그래프가 도출됩니다. 이에 대해서 하나씩 살펴보겠습니다.

02. Causal Discovery를 위한 가정

Causal Discovery는 세 가지 가정이 필요합니다.

Acyclicity (for DAG) Assumption
Causal Markov Assumption
Faithfulness Assumption

Acyclicity 가정은 DAG 그래프를 활용하기 때문에 설명을 생략하고, 나머지 가정에 대해서 알아보겠습니다.

Causal Markov Assumption

확률 변수 $X_1$, $X_2$, $X_3$의 Joint Distribution은 $P(X_1, X_2, X_3)=P(X_1)P(X_2|X1)P(X_3|X_1,X_2)$로 표현할 수 있습니다. 만약 아래와 같이 그래프가 주어지면 어떨까요?

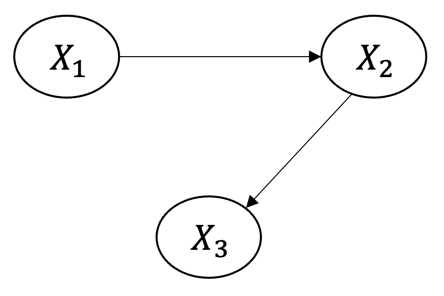
Causal Markov Assumption은 이와 같이 인과그래프가 주어졌을 때, 특정 노드는 자신에게 직접적으로 영향을 주는 노드에게만 종속되며, 이외의 모든 노드들과는 독립이라는 가정입니다. 이를 수식으로 $P(X_1, X_2, X_3)=P(X_1)P(X_2|X1)P(X_3|X_2)$로 표현할 수 있습니다. 즉, $X_3$는 $X_2$에만 직접적인 영향을 받고, $X_1$으로부터는 간접적으로만 영향을 받기 때문에 수식의 $P(X_3|X_2)$ 부분이 바뀐 것을 볼 수 있습니다.

Faithfulness Assumption

아래와 같은 그래프를 가정해보겠습니다.

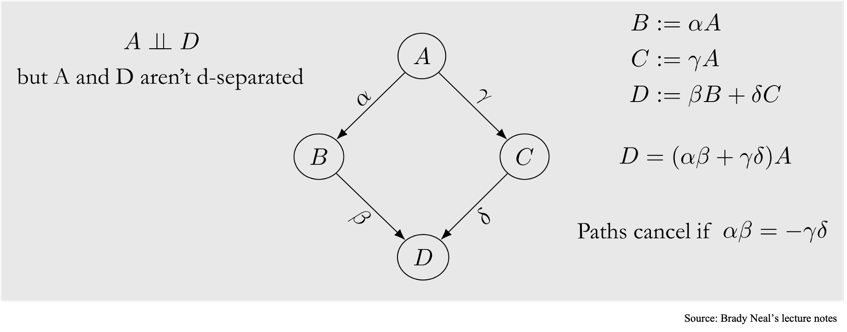
faithfulness

노드 $A$와 노드 $D$는 d-connected 되어있습니다. $A \rightarrow B \rightarrow D$의 경로와 $A \rightarrow C \rightarrow D$ 경로가 존재하기 때문이죠. 그런데 만약, $A \rightarrow B \rightarrow D$의 경로와 $A \rightarrow C \rightarrow D$ 경로가 각각 서로의 효과를 상쇄하는 정반대의 인과적 효과를 낸다면 어떻게 될까요? 예를 들어서, $A \rightarrow B \rightarrow D$의 경로는 $+1$의 인과적 효과를, $A \rightarrow C \rightarrow D$의 경로는 $-1$의 인과적 효과를 낸다면, 둘의 효과가 상쇄될 것입니다. Faithfulness Assumption은 이러한 효과는 존재하지 않으며, 따라서 경로 내에 있는 노드들은 반드시 종속적인 관계여야 한다고 가정합니다.

위와 같은 가정을 마쳤으면, Causal Discovery 알고리즘을 적용하여 인과 그래프를 도출할 수 있습니다.

03. 다양한 Causal Discovery 알고리즘

인과 그래프를 도출할 수 있는 Causal Discovery 종류는 아래와 같이 굉장히 다양합니다.

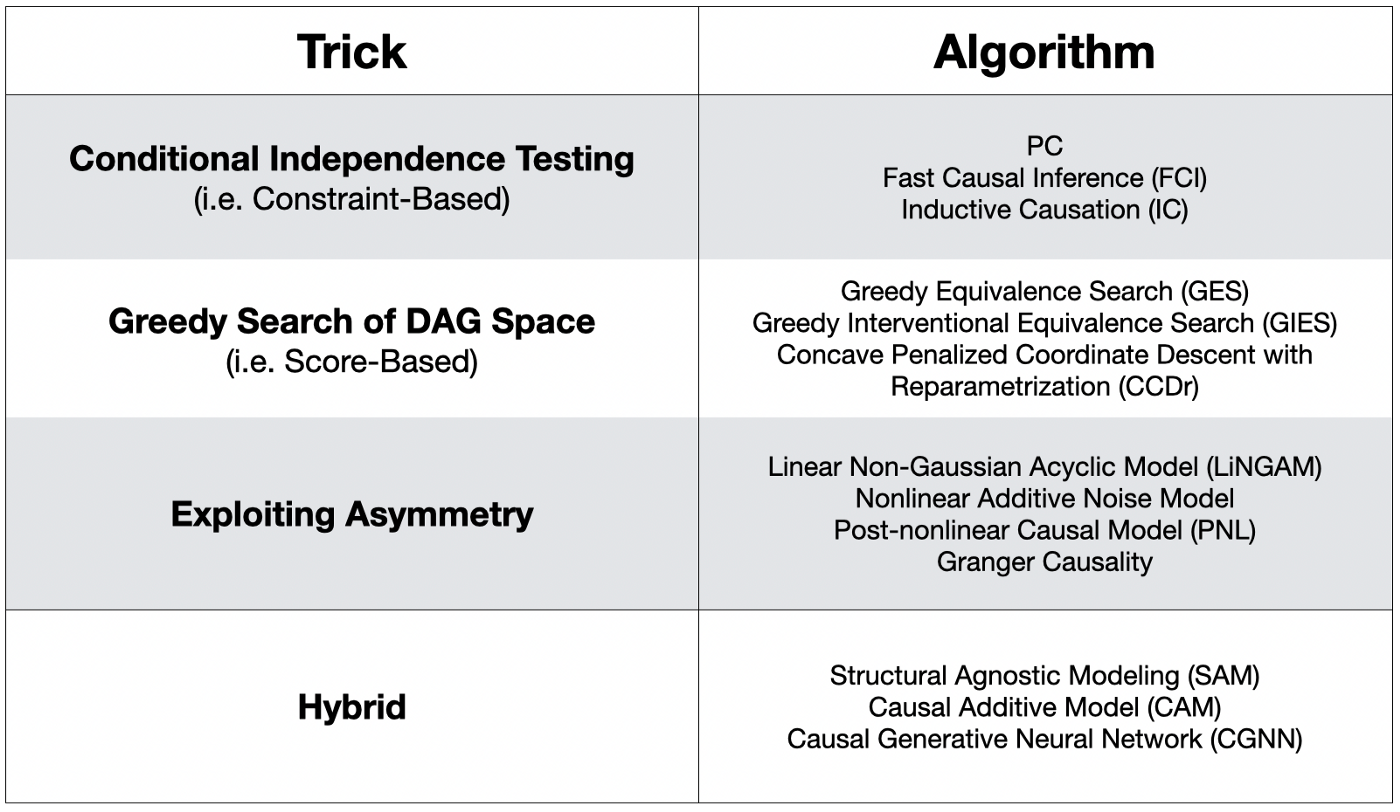causal discovery algorithms (참고) 이 표는 여기에서 가져왔습니다.

이들 중 어떠한 알고리즘이 특별히 다른 알고리즘보다 뛰어나다고 하기는 어렵습니다. 다만, 구현하는 방식에서의 디테일들이 다릅니다. 그리고 가장 유명한 알고리즘이자, 필자로 하여금 인과추론을 공부하게 했던 알고리즘이 바로 Conditional Independence 가정을 활용하는 PC 알고리즘 입니다.

PC 알고리즘을 이해하기 위해서 먼저 한 가지 더 알아야할 것이 있는데요. Markov Equivalence Class가 그것입니다.

04. Markov Equivalence Class

Markov Equivalence Class란, 동일한 skeleton과 V-structure를 가지며, 동일한 Conditional Dependency를 가지는 그래프들의 집합으로 정의할 수 있습니다. 말이 어렵지만, 그림을 보며 이해하면 쉽게 알 수 있습니다.

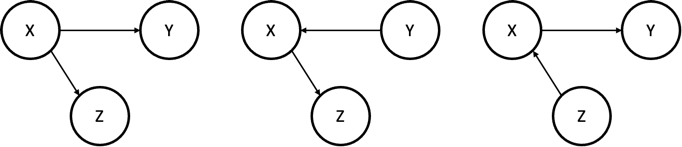
Markov Equivalence Class 01

위의 세 그래프는 모두 동치(Equivalent)하다고 할 수 있습니다. 왜냐하면, 세 그래프 모두 $X$와 $Z$ 및 $X$와 $Y$ 간의 관계는 직접적으로 연결되어 있어서 서로 Dependent하고, $Y$와 $Z$는 $X$를 통해서 연결되어 있어서 서로 Dependent하며, $X$를 Conditioning 하면 $Y$와 $Z$가 Conditionally Independent 해지는 구조이기 때문입니다.

이렇게 $X$, $Y$, 그리고 $Z$로 표현할 수 있는 모든 DAG 그래프는 다음과 같습니다.

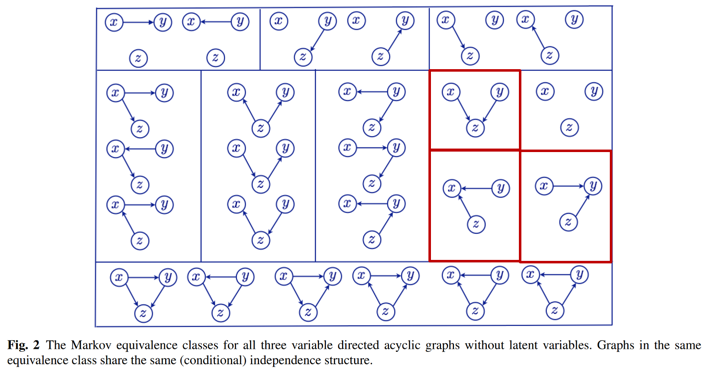
Markov Equivalence Class 02

즉, 데이터의 Joint Distribution 내에 존재하는, 노드들 간 하나의 종속(또는 독립) 관계들로 그려낼 수 있는 동치 그래프가 이렇게 여러 개 존재한다는 것입니다. 문제는, 이와 같이 하나의 종속(또는 독립) 관계로 여러 그래프가 도출된다면, 이 중 어떤 그래프가 옳은 인과 그래프인지 특정할 수 없게됩니다.

여기서 빨간색 박스 부분을 주목해야 합니다. Collider로 V-structure를 이루고 있는 모양이죠. Collider 꼴로 이루어진 노드 간 종속 관계는 동치인 그래프가 여러 개 존재하지 않고, 단 하나의 그래프만이 존재합니다. 즉, Collider 꼴은 노드 간 종속(또는 독립) 관계를 확인할 수 있다면, 단 하나의 인과 그래프로 특정할 수 있는 구조라는 것입니다. 이러한 이유로 인해 Collider 구조는 Causal Discovery에서 핵심적인 역할을 합니다.

05. PC 알고리즘

PC 알고리즘은 이를 개발한 Peter Spirtes와 Clark Glymour의 이름을 따서 만들어졌습니다. 이는 확률적으로 독립인 두 변수는 인과적으로 연결되어있지 않다는 아이디어를 기반으로 합니다. 앞서 Causal Discovery를 위한 가정과 Markov Equivalence Class 및 Collider(V-structure) 구조의 중요성을 인지했다면, PC 알고리즘 또한 쉽게 이해할 수 있습니다.

그럼, PC 알고리즘을 차근차근 살펴보겠습니다.

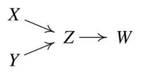Ground Truth 그래프

우리가 PC 알고리즘을 이용하여 궁극적으로 도출하고 싶은 Ground Truth 그래프는 위와 같다고 합시다.

STEP 01

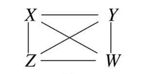PC step 01 PC 알고리즘 STEP 01

첫번째 단계는 모든 노드들이 완전히 연결되어 있는 Complete Undirected Graph로 시작합니다.

STEP 02

두번째 단계에서는 노드 간 Conditionally Independent한지 여부를 확인하여 Unconditionally Independent한 노드 사이의 간선을 제거합니다. 예를 들어서, Ground Truth 그래프를 보았을 때, $X$와 $Y$는 어떠한 Conditioning을 수행하지 않는다 하더라도 서로 독립입니다. 이러한 관계를 Unconditionally Independent 하다고 표현합니다. 해당 노드 사이의 간선을 제거합니다. 그 결과는 다음과 같습니다.

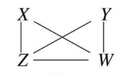PC step 02 PC 알고리즘 STEP 02

STEP 03

세번째 단계에서는 두 노드 간 다른 노드가 있는 경우, 사이에 있는 노드를 Conditioning 해보았을 때 두 노드가 Conditional Independent하다면, 두 노드 사이의 간선을 제거합니다. 예를 들어, STEP 02에서 $X-Z-W$ 경로에서 $Z$를 Conditioning 했더니 $X$와 $W$가 Independent 해졌다고 합시다. 그러면 $X-W$ 사이의 간선이 제거됩니다. 이러한 과정을 반복하고 나면, 아래 그림과 같이 Skeleton이라 부르는 뼈대가 형성됩니다.

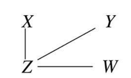PC step 03 PC 알고리즘 STEP 03, Skeleton

STEP 04

네번째 단계에서는 Markov Equivalence Class에서 살펴보았던 V-structure 구조를 이용합니다. 앞서 보았듯, Collider의 V-structure 구조는 동치인 여러 그래프가 도출되는 것이 아닌 단 하나의 그래프만 도출됩니다. 이를 이용하여 Skeleton을 유향 그래프로 바꾸어 줍니다.

예를 들어, STEP 03의 Skeleton을 보면, ($X-Z$, $Y-Z$), ($Y-Z$, $W-Z$), ($X-Z$, $W-Z$) 쌍으로 $Z$를 향해 화살표를 그어봄으로써 Collider를 만들 수 있습니다. 그런데 이러한 경우의 수 중 ($Y \rightarrow Z$, $W \rightarrow Z$) 또는 ($X \rightarrow Z$, $W \rightarrow Z$)로 Collider를 만들 경우, $Z$를 Conditioning 했을 때, 두 노드 간 Dependency가 생기지 않고, Independent한 관계가 되기 때문에 Collider가 될 수 없습니다. 따라서 $Z$를 Conditioning 했을 때 두 노드인 $X$와 $Y$ 간 Dependency가 생기는 ($X \rightarrow Z$, $Y \rightarrow Z$) 구조로 Collider를 만들 수 있습니다.

이러한 방식으로 Collider를 만들어가면 아래와 같은 그래프가 나타납니다.

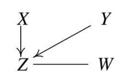PC step 04 PC 알고리즘 STEP 04

STEP 05

마지막 절차는 Orientation Propagation으로 불립니다. 남아있는 무방향 간선들을 활용하여 Collider가 되지 않는 쪽으로 방향을 설정해줍니다. 그 결과 아래와 같이 Ground Truth와 유사한 인과 그래프를 도출할 수 있습니다.

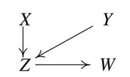PC step 05 PC 알고리즘 STEP 05

06. PC 알고리즘 활용해보기

PC 알고리즘은 Causal Discovery Toolbox 파이썬 라이브러리를 사용하여 돌려볼 수 있습니다. 다음 예제는 여기를 참고했음을 먼저 밝힙니다.

이 예제에서는 1994년 미국의 Census Income Data Set 데이터를 활용합니다. 데이터의 대략적인 생김새는 다음과 같습니다.

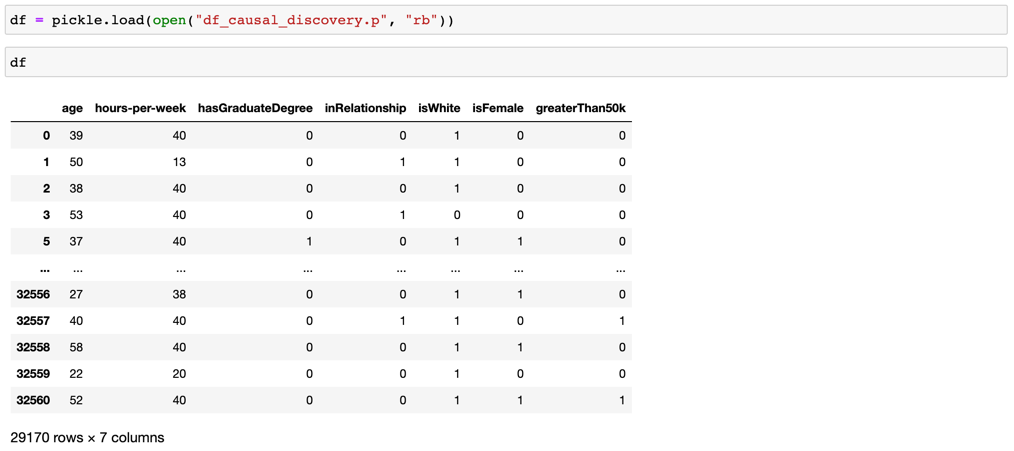
census_dataset

코드와 실행 결과는 다음과 같습니다.

  
# 라이브러리를 임포트함
import pickle
import cdt
import networkx as nx
import matplotlib.pyplot as plt

# 데이터를 불러옴
df = pickle.load( open( "df_causal_discovery.p", "rb") )

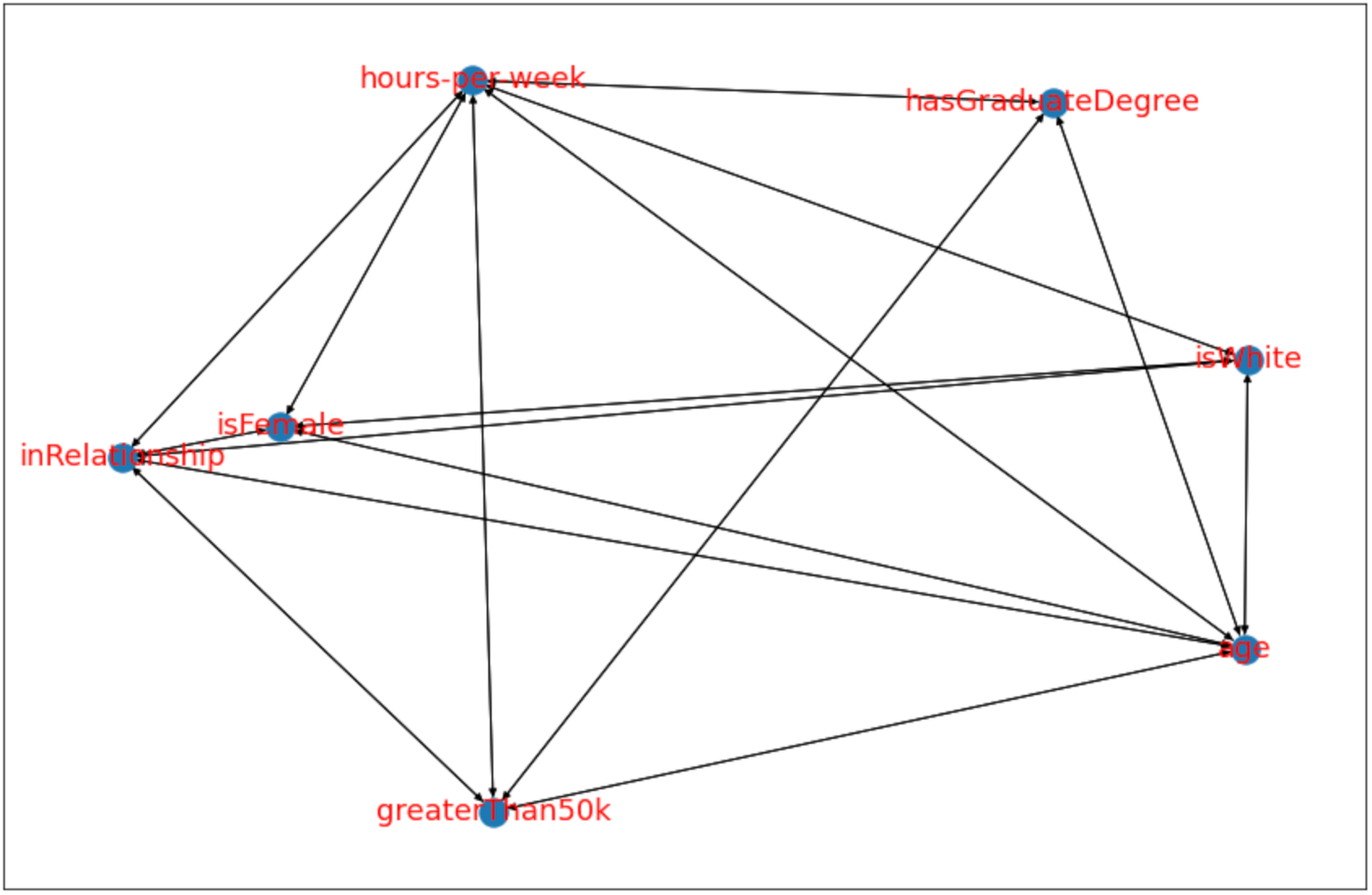
# Skeleton 그래프를 그림
glasso = cdt.independence.graph.Glasso()
skeleton = glasso.predict(df)

# 그래프를 시각화함
fig = plt.figure(figsize=(15,10))
nx.draw_networkx(skeleton, font_size=18, font_color='r')

result_skeleton

  
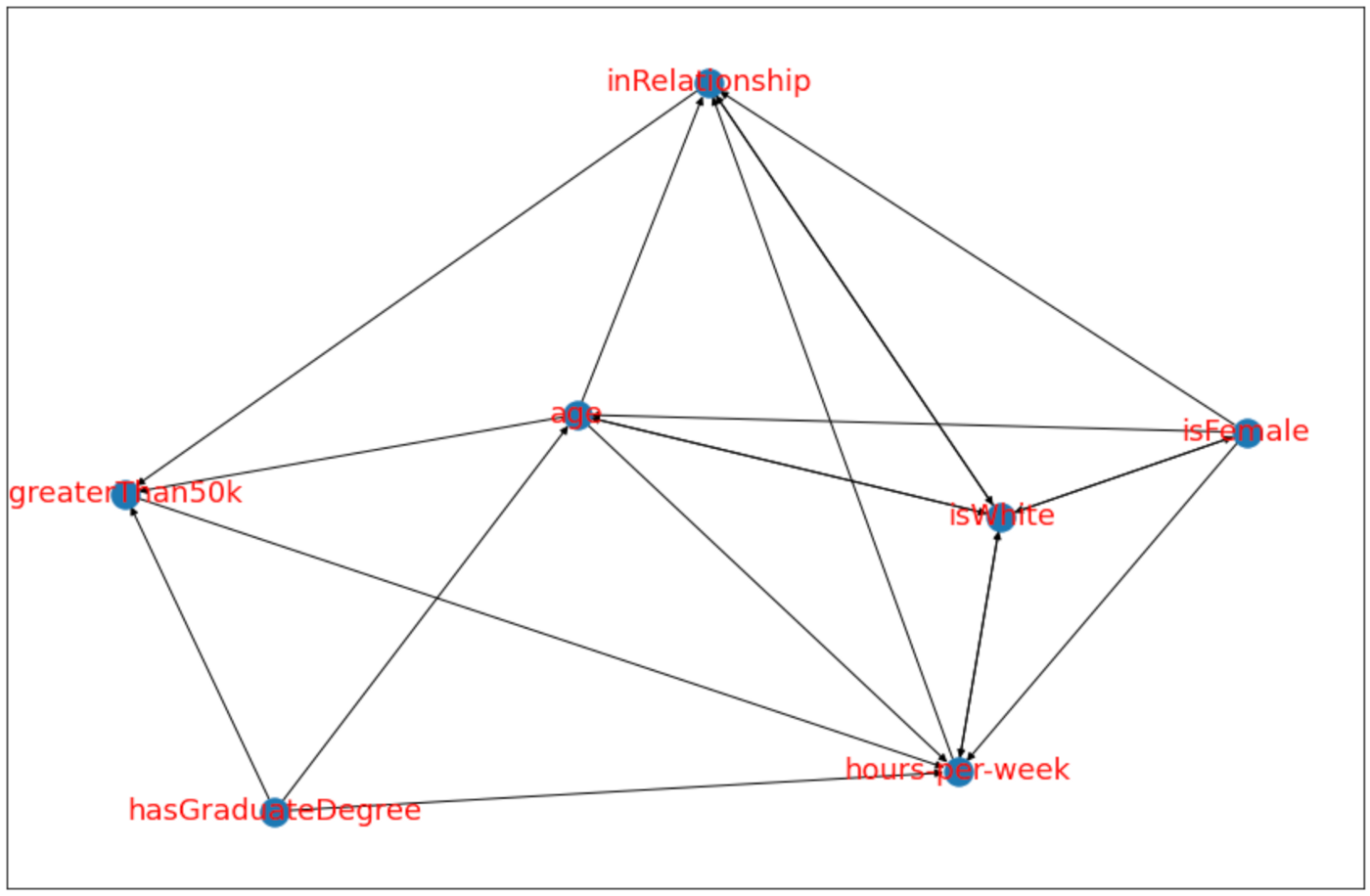
# Causal Discovery를 활용함

# PC 알고리즘
model_pc = cdt.causality.graph.PC()
graph_pc = model_pc.predict(df, skeleton)

# 그래프를 시각화함
fig=plt.figure(figsize=(15,10))
nx.draw_networkx(graph_pc, font_size=18, font_color='r')

result_PC

07. 정리하며

이번 포스트에서는 Causal Discovery와 PC 알고리즘에 대해서 알아보았습니다. 인과 그래프를 먼저 구축한 후 인과관계를 추론하는 기존의 방법과는 달리, 데이터를 바탕으로 인과 그래프 자체를 도출하는 Causal Discovery는 아직도 학계에서 많은 연구가 이루어지고 있는 분야입니다.

아쉽게도 Causal Graph 자체를 정확하게 검증할 수 있는 방법은 세상에 없다고 합니다. 그만큼 훗날, Causal Discovery 방법론들이 이러한 한계점을 극복할 수 있는 대안이 될 수 있을 것입니다.

참고자료

[1] 인과추론의 데이터과학
[2] Introduction to Causal Inference (Brady Neal)
[3] Causal Discovery- Shawhin Talebi의 블로그

Causal Discovery와 PC 알고리즘