이 포스트는 개인적으로 공부한 내용을 정리하고 필요한 분들에게 지식을 공유하기 위해 작성되었습니다.
지적하실 내용이 있다면, 언제든 댓글 또는 메일로 알려주시기를 바랍니다.
베이즈 정리
💡 확률론 패러다임의 전환 : 연역적 추론에서 귀납적 추론으로
베이즈 정리의 공식
$ P(H|E)=\cfrac{P(E|H)P(H)}{P(E)} $
H(Hypothesis) : 가설 혹은 ‘어떤 사건이 발생했다는 주장’E(Evidence) : 새로운 정보- 베이즈 정리는 두 확률 번수의 사전 확률과 사후 확률 사이의 관계를 나타내는 정리임
- 사전 확률 $P(H)$ : 아직 사건 E에 관한 어떠한 정보도 알지 못하는 것을 의미함
- 어떤 사건이 발생했다는 주장에 관한 신뢰도
- 사후 확률 $P(H|E)$ : 사건 E 값이 주어진 경우에 대한 H의 사후 확률
- 새로운 정보를 받은 후 갱신된 신뢰도
- 사전 확률 $P(H)$ : 아직 사건 E에 관한 어떠한 정보도 알지 못하는 것을 의미함
베이즈 정리를 이해하기 어려웠던 이유
- 빈도 주의(frequentism)의 확률 관점에 익숙하기 때문임
- 빈도 주의와 베이지안 주의
- 빈도 주의 : “100번 동전을 던졌을 때 50번은 앞면이 나온다.”
- 베이지안 주의 : “동전의 앞면이 나왔다는 주장의 신뢰도가 50%다.”
- 확률을 ‘주장에 대한 신뢰도’로 해석하는 관점
빈도 주의 (기존의 통계학)
- 연역적 사고에 기반
- 확률 계산, 유의성 검정
- 엄격한 확률 공간을 정의하거나 집단의 분포를 정의하고 파생 결과물을 수용함
베이지안 주의 (새로운 통계학)
- 귀납적 추론 방법
- 확률은 빈도 주의 방식으로 계산되는 것이 아니라, ‘믿음의 정도(Degree of belief)’로 정의되어 믿음을 수량화한 개념으로 봄
- 더욱 다양한 상황에 확률을 부여할 수 있음 (빈도 주의로는 모든 것을 무한히 시행할 수 없으므로)
- 추가되는 정보를 바탕으로 사전 확률 $P(H)$를 $P(H|E)$로 갱신함
- 추가 근거 확보를 통해 진리로 더 다가갈 수 있다는 철학을 내포함
예제 1
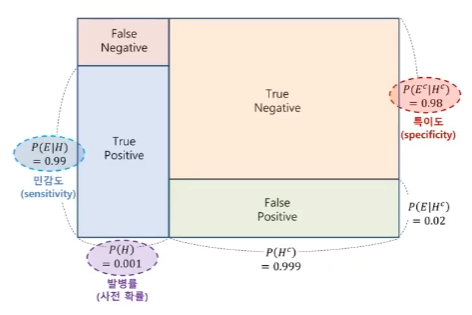
질병 A의 발병률은 0.1%로 알려져있다. 이 질병이 실제로 있을 때 질병이 있다고 검진할 확률(민감도)은 99%, 질병이 없을 때 실제로 질병이 없다고 검진할 확률(특이도)는 98%라고 하자. 만약 어떤 사람이 질병에 걸렸다고 검진 받았을 때, 이 사람이 정말로 질병에 걸렸을 확률은?
- Hypothesis H : 실제로 병이 있다.
- $P(H)=0.001$
- Evidence E : Positive로 병을 진단 받았다.
- $P(E|H)=0.99$
- $P(E^c|H^c)= 0.98$
$ P(H|E)=\cfrac{P(E|H)P(H)}{P(E)} $
- 이때 우리는 $P(E)$를 모르는데 $P(E)$는 $P(E|H)P(H) + P(E|H^c)P(H^c)$로 계산할 수 있으며, 이는 파란 박스와 초록 박스 영역에 해당됨
$ P(H|E)=\cfrac{P(E|H)P(H)}{P(E|H)P(H) + P(E|H^c)P(H^c)} $
$ P(H|E)=\cfrac{0.001 \times 0.99}{0.001 \times 0.99 + 0.999 \times 0.02} = 0.047 $
- 47% 정도의 신뢰도로 질병에 걸렸다고 보는 것임
예제 2
예제 1에서 한 번 양성 판정을 받았던 사람이 두 번째 검진을 받고 또 양성 판정을 받았을 때, 이 사람이 실제로 질병에 걸린 확률은?
- 우리가 원래 알고 있던 발병률은 사전 확률 $P(H)=0.001$이었는데, 증거 E를 가지고 새로 알게된 정보에 따르면, 사후 확률 $P(H|E)=0.047$로 주장에 대한 신뢰도가 갱신되었음
- 예제 2에서는 사후 확률 $P(H|E)=0.047$가 사전 확률 $P(H)=0.047$로써 사용됨
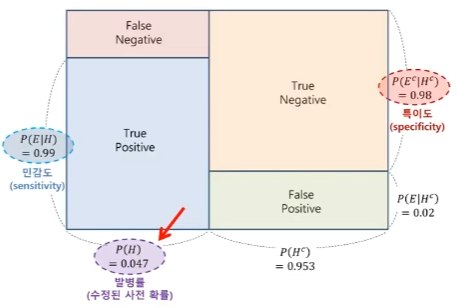
- 예제 1에서와 동일한 방식으로 계산하되, 수정된 사전 확률로써 계산하면 아래와 같음
$ P(H|E)=\cfrac{P(E|H)P(H)}{P(E|H)P(H) + P(E|H^c)P(H^c)} $
$ P(H|E)= \cfrac{0.047 \times 0.99}{0.047 \times 0.99 + 0.953 \times 0.02}=0.709 $
- 70% 정도의 신뢰도로 질병에 걸렸다고 보는 것임
정리
- 데이터가 사전 확률을 사후 확률로 업데이트함
- 새로운 데이터를 반영할 수 있음
- 사전 분포 적용을 통해 기존 지식의 통합이 가능함
- 모수 공간을 줄이는 효과
- 데이터를 직접 반영하여 사후 분포를 구성함 (빈도 주의와의 차이)
- 모수가 많고 복잡한 모델까지 추론 가능함
참고
[1] 공돌이의 수학정리노트
[2] [스탠코리아 StanKorea] 베이즈 통계학 소개 Introduction to Bayesian Statistics | 베이즈 정리 & 베이즈 추론 | 베이지안이 되어야 할 이유