이 포스트는 개인적으로 공부한 내용을 정리하고 필요한 분들에게 지식을 공유하기 위해 작성되었습니다.
지적하실 내용이 있다면, 언제든 댓글 또는 메일로 알려주시기를 바랍니다.
본 포스트의 상당 내용은
인과추론의 데이터과학강의를 정리한 것임을 밝힙니다.
지난 이야기
복잡한 IT 환경에서 이상징후 및 장애가 발생되었을 때, 이를 인과추론의 방식으로 해결해보고자 하는 큰 꿈을 품고 첫 포스트인 공부하며 정리하는 인과추론 01을 올렸습니다. 기계학습 기법에 익숙했던 필자에게는 다소 생소한 데이터 분석 분야라는 것을 알게되었고, 어렵지만 차근차근 공부하며 정복해보고자 하는 욕심이 생겼습니다. 또한 추천시스템 도입 사례와 심슨의 역설 예제를 통해서 인과관계를 어떻게 정의하는지에 따라 인과추론 결과가 달라질 수 있다는 점도 살펴보았습니다.
이번 포스트에서는 인과추론의 양대산맥인 Potential Outcomes Framework와 Structural Causal Model(SCM)의 개괄을 살펴보려 합니다. 이번 포스트도 역시나 인과추론을 처음 접하는 필자가 인과추론의 데이터과학 강의를 듣고 해당 내용을 중심으로 정리합니다. 따라서 자세한 내용은 해당 강의를 보시길 추천드립니다.
인과추론의 양대산맥
인과관계를 알아내기 위한 인간의 고민은 아리스토텔레스 시대까지도 거슬러 올라갈 수 있을 만큼 굉장히 오래된 역사를 가진다고 합니다(참고). 인간의 사유에 근거한, 철학적인 접근으로 인과관계가 무엇인지 고민했던 것이죠. 현대는 데이터의 시대입니다. 이에 따라, 인간의 사유에만 의존했던 과거의 철학적 접근 방식을 너머, 더욱 시스템적이고 과학적인 방법으로 인과관계를 분석하려는 방식이 개발되었습니다.

위 그림이 바로 그것인데요. 이들은 인과추론의 양대산맥으로, 왼쪽은 Potential Outcomes Framework라는 인과추론 방식이며, 오른쪽은 Structural Causal Model이라는 인과추론 방식입니다. Potential Outcomes Framework는 하버드의 Donald Rubin 교수님이 만든 방법이며, Structural Causal Model은 UCLA의 Judea Pearl 교수님이 개발했다고 합니다. 무엇이 다를까요? 구체적인 방법론의 상세 내용은 추후에 하나씩 다루겠지만, 지금은 간략하게만 짚고 가봅시다.
Potential Outcomes Framework는 ‘만약 타임머신을 타고 과거로 돌아갔는데 그 원인이 없었더라면 현재 결과는 어땠을까?’라는 관점에서 인과관계를 정의합니다. 제목 그대로 Potential Outcome, 즉, 잠재적 결과를 이용하여 인과관계를 보려는 것이죠. 반면에, Structural Causal Model은 인과관계로 표현할 수 있는 변수들을 인과그래프로 모델링한 후, 인과관계를 분석해보려는 시도입니다.
이 두 방법 중 어느 방법이 특별히 더 우수하다거나 상호배타적인 관계라고 할 수는 없습니다. 다만, 결이 다른 접근 방법이라고 보면 좋을 것 같습니다. Potential Outcomes Framework의 경우, 해당 방법론의 초석을 다진 연구자들이 최근 노벨 경제학상을 받았다고 합니다. 한편, Structural Causal Model을 개척한 Judea Pearl 교수님은 컴퓨터과학 분야에서 가장 권위 있는 상인 Turing Award를 수상했다고 합니다. 이러한 단편적인 예만 보아도 두 방식의 차이가 있는데, 전자는 사회과학 분야를 바탕으로 발전되어 왔으며, 후자는 컴퓨터과학 분야를 바탕으로 발전되었다고 합니다. 중요한 것은, 결이 다른 두 방법론을 잘 이해하고, 우리가 풀고자 하는 문제에 더 적합한 방법론이 무엇인지 결정하여 잘 활용하는 데 있습니다.
훑어보는 Potential Outcomes Framework
앞서, Potential Outcomes Framework는 잠재적 결과를 이용하여 인과관계를 분석한다고 했습니다. 이 말에 대해서 조금 더 들여다보도록 하죠.

Counterfactual과 Control Group
‘독서가 성적에 미치는 영향’을 심슨가족 캐릭터로 예를 들어봅시다. 위 그림의 왼쪽을 보았을 때, 책을 읽고 있는 리사(여자)가 진짜 책을 읽었기 때문에 성적이 올랐는지를 Potential Outcomes Framework 관점에서 분석하려 합니다. 그러면 리사가 (1)책을 읽은 후 받은 성적과 (2)타임머신을 타고 책을 읽기 전으로 돌아간 후, 이번에는 책을 읽지 않아본 상태로 받은 성적을 비교해보아야 합니다. 이때 전자를 (1)실제 결과라고 하고, 후자를 (2)잠재적 결과(Potential Outcome)라 하며, 실제 결과와 잠재적 결과의 차이인 (1)-(2)를 처방(Treatment)의 인과적 효과(Causal Effect)라고 합니다. 또한 (2)잠재적 결과를 실제 (1)이라는 사실과 반대되는 사실이라 하여 반사실(Counterfactual)이라고 부릅니다. 아래와 같이 표현할 수 있습니다.
Causal effect of the treatment
= (Actual outcome for treated if treated) - (Potential outcome for treated if not treated (i.e., Counterfactual))
사실 여기에는 문제가 있습니다. 현실 세계에서는 타임머신이 존재하지 않기 때문에 실제로는 잠재적 결과를 관측할 수 없다는 점입니다. 이러한 문제를 Fundamental Problem of Causal Inference라고 부릅니다.
이처럼 우리는 현실에서 반사실에 대한 잠재적 결과를 관측할 수 없기 때문에 대안을 찾아야 합니다. 그 대안은 나와 다른 행동을 한 집단인 Control Group을 관측해보는 것입니다. 위 그림의 오른쪽으로 예를 들어보자면, 리사(여자)가 진짜 책을 읽었기 때문에 성적이 올랐는지를 분석하기 위해서 책을 읽지 않은 다른 사람, 즉 바트(남자)와 비교하는 것입니다. 즉, 바트가 Control Group이 되는 것이죠. Control Group인 바트가 책을 읽지 않고 받는 성적은 관측 가능하기 때문에, 책을 읽은 리사의 성적과 비교 가능할 것입니다. 아래와 같이 표현할 수 있습니다.
Observed effect of the treatment
= (Actual outcome for treated if treated) - (Actual outcome for untreated if not treated (i.e., Control Group))
선택편향(Selection Bias)
그렇다면, 실제 결과와 ‘Counterfactual의 잠재적 결과’가 아닌, ‘Control Group의 실제 결과’를 비교하는 방식이 동일한 인과적 효과를 낼 것이라고 확신할 수 있을까요? 분명히 차이가 있을 수밖에 없을 것입니다. 예를 들어, 리사가 책을 읽었기 때문에 책을 읽지 않은 Control Group인 바트보다 성적이 잘 나온 것인지, 아니면 애초에 리사가 너무나 똑똑해서 책을 읽지 않았어도 성적이 잘 나왔을 것인지 명확하게 말하기 어렵습니다. 이처럼, 나와 ‘나의 반사실에 대한 잠재적 결과’가 아닌 ‘남의 결과’를 비교하면서 발생하는 차이를 선택편향(Selection Bias)라고 합니다. 아래와 같이 분해하여 표현할 수 있습니다.
Observed effect of the treatment (decomposition)
= (Outcome for treated if treated) - (Outcome for untreated if not treated (i.e., Control Group))
= (Outcome for treated if treated)
- (Outcome for treated if not treated) + (Outcome for treated if not treated) # Zero Some
- (Outcome for untreated if not treated)
= (Outcome for treated if treated) - (Outcome for treated if not treated) # Causal Effect
+ (Outcome for treated if not treated) - (Outcome for untreated if not treated) # Selection Bias
= Causal Effect + Selection Bias
비교할 수 있는 Control Group 찾기 (Ceteris Paribus)
앞서, 관측 가능한 Control Group을 이용하여 비교하면 선택편향이 발생하기 때문에 정확한 인과추론이 어려워진다는 것을 살펴보았습니다. 그럼 선택편향 자체를 없앨 수만 있다면 관측 가능한 Control Group을 이용하면서도 인과추론이 가능해지지 않을까요?
만약, Control Group이 반사실 집단, 즉, Counterfactual과 동일하다면, 선택편향은 사라질 것입니다. 즉, Counterfactual과 최대한 비슷하게 Control Group을 구성하면, 선택편향이 최소화되어 Control Group을 Counterfactual를 대신하여 비교할 수 있다는 것입니다. 이는 Control Group을 구성할 때, 타임머신을 타고 과거로 돌아가서 원인이 되는 일을 내가 실제로 행하였는지(즉, 처방을 받았는지(treated)) 여부만 제외하고 Counterfactual과 모든 조건을 동일하게 설정하면 됩니다. 이처럼 나머지 모든 조건을 동일하게 둔다는 설정을 라틴어로 Ceteris Paribus라고 합니다. 이와 같이 Potential Outcomes Framework는 Counterfactual과 가장 가까운 Control Group을 찾아낼 수 있도록 연구 디자인을 고안하는 접근 방식을 취합니다.
하지만 Ceteris Paribus를 만족하는 설정으로 Control Group을 구성하는 것 또한 쉬운 일이 아닙니다. 왜냐하면, 현실 세계에서는 우리가 관측하고자 하는 Control Group을 구성하는 Selection Process를 완벽하게 통제하기 어렵기 때문입니다.
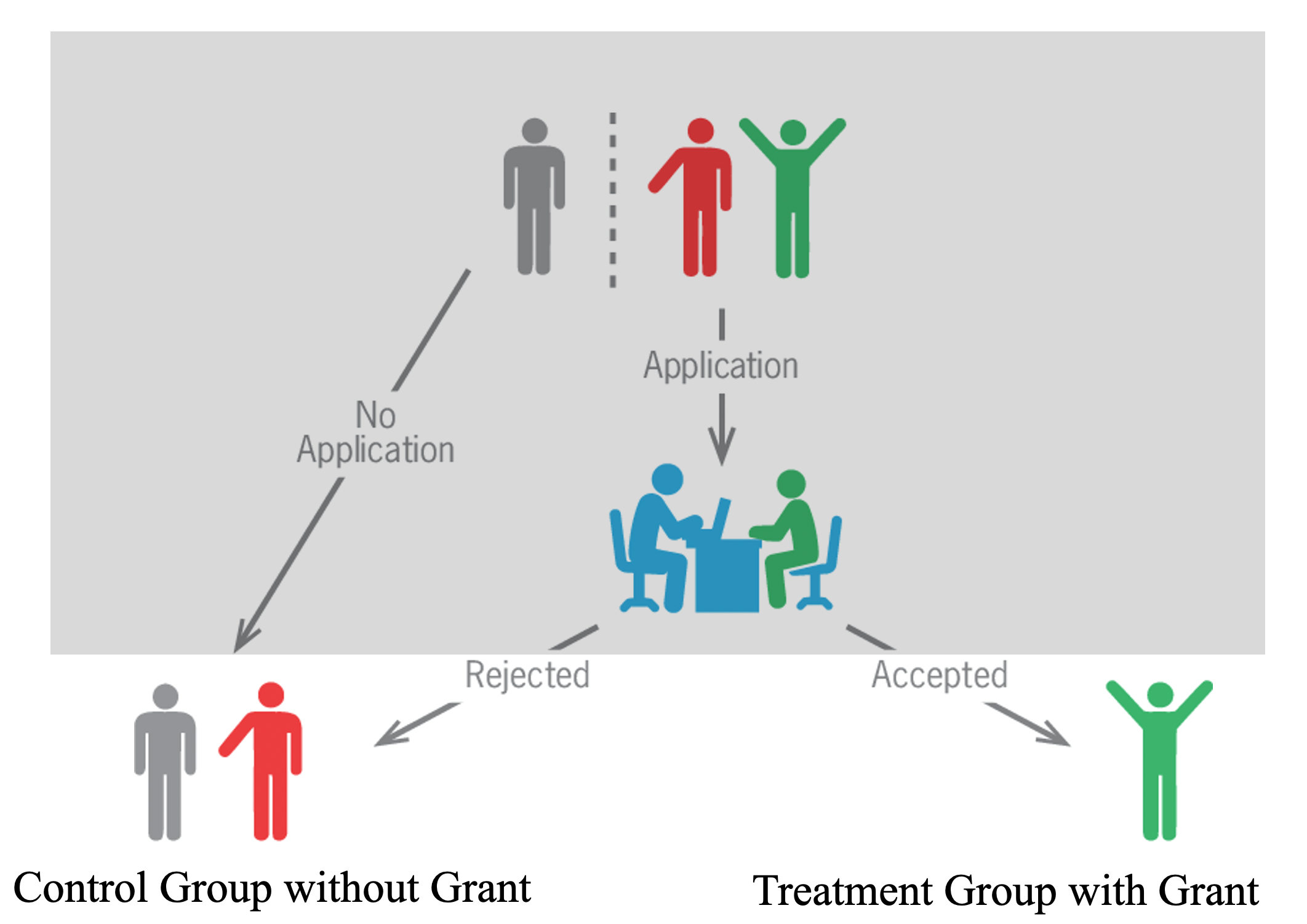
위 그림은 보조금을 받은 집단과 보조금을 받지 못한 Control Group을 구성하는 과정을 나타내는 예입니다. 주목할 것은, Control Group으로 구성된 보조금을 받지 못한 집단의 경우, 보조금 자체를 신청하지 않은 사람도 있겠으나, 어떤 이유에서든지 보조금을 지원했는데 탈락하여 받지 못한 사람도 있을 수 있다는 것입니다. 이 경우, 같은 Control Group에 속해있는 사람이라 해도 그 성격이 매우 다를 것이고, 결과적으로 이렇게 구성된 Control Group으로는 Cetris Paribus를 만족하기 어려울 것입니다. 결과적으로 인과관계에 대한 추론은 더욱더 어려워질 것입니다.
한편, Selection Process를 완전하게 통제할 수 있는 이상적인 경우가 있기는 합니다. 바로 Control Group을 구성하는 방식을 동전 던지기로 결정하는 등 완전히 무작위로 정하면 되는데요. 이 방법은 머릿속에서 상상하기로 가장 이상적으로 Counterfactual과 가까운 Control Group을 구성할 수 있겠지만, 윤리적 문제나 실현 불가능성 등의 이유로 현실에서 활용하기 어렵습니다. 예를 들어, 담배와 폐암의 인과관계를 보기 위해 Control Group을 무작위로 뽑은 후 흡연을 강제할 수는 없겠죠.
정리하자면, Potential Outcomes Framework는 무작위로 Control Group을 구성하여 비교하면 인과관계를 쉽게 도출할 수 있겠지만, 현실적으로 어려우니, 이를 대신할 수 있는 적절한 연구 디자인을 고민함으로써 인과관계를 추론한다고 이해하면 좋을 것 같습니다. 이에 대한 방법론도 무척 많지만, 기회가 되면 다음 포스트에서 다루겠습니다.
훑어보는 Structural Causal Model(SCM)
Causal Inference의 또다른 양대산맥으로 볼 수 있는 Sturctural Causal Model 또한 간략하게 훑어보겠습니다. Structural Causal Model은 기본적으로 Bayesian Network를 활용하여 인과관계를 표현하고 추론하는 접근방식입니다.
Bayesian Network란, 랜덤 변수의 집합과 유향 비순환 그래프(Directed Acyclic Graph, DAG)를 통하여 그 집합을 조건부 독립으로 표현하는 확률 그래픽 모델입니다. 말이 어렵네요. 자세한 내용은 추후에 다루도록 하고, 간단하게 그래프의 노드는 변수를, 엣지(화살표)는 인과관계를 표현한다고 생각하고 넘어갑시다.
Causal Graph
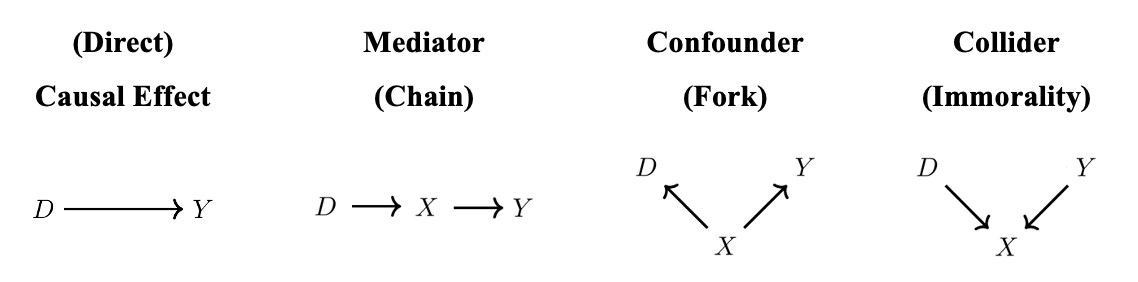
위 그림은 유향 비순환 그래프로 인과관계를 표현한 Causal Graph의 종류입니다. 각각을 해석하면 다음과 같습니다.
(Direct) Causal Effect- 원인 변수 $D$가 결과 변수 $Y$에게 직접적으로 영향을 주는 경우입니다.
Mediator (Chain)- 원인 변수 $D$가 어떠한 중재 변수 $X$를 통하여 결과 변수 $Y$에게 간접적으로 영향을 주는 경우입니다.
Confounder (Fork)- 변수 $D$와 변수 $Y$에 영향을 주는 공통 변수(Common Cause) $X$가 존재하는 경우입니다. 이때 $X$는
Confounder(교란요인)이라고 부르기도 합니다. - 예시는 다음과 같습니다.
- ($X$ -> $D$ 예시) 술을 마셔서 신발을 신고 잠을 잤다.
- ($X$ -> $Y$ 예시) 술을 마셔서 다음 날 머리가 아프다.
- 변수 $D$와 변수 $Y$에 영향을 주는 공통 변수(Common Cause) $X$가 존재하는 경우입니다. 이때 $X$는
Collider (Immorality)- 변수 $D$에도 영향을 받고 변수 $Y$에도 영향을 받는 공통의 결과 변수 $X$가 존재하는 경우입니다.
- 예시는 다음과 같습니다.
- ($D$ -> $X$ 예시) 야간 교대근무를 하면 너무 졸리다.
- ($Y$ -> $X$ 예시) 수면 무호흡증 때문에 잘 못 자면 너무 졸리다.
아래의 그림은 위와 같이 표현될 수 있는 Causal Graph에서 어떻게 연관성(Association)을 해석할 수 있는지 보여줍니다.
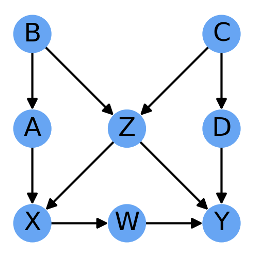
먼저, $B$ -> $A$ -> $X$를 보면, $B$노드는 원인이 되어 $A$노드를 거쳐서 $X$노드의 결과로 작용됩니다. 한편, $B$ -> $Z$ -> $Y$를 보면, $B$노드는 원인이 되어 $Z$노드를 거쳐서 $Y$노드의 결과로 작용됩니다. 즉, $X$노드와 $Y$노드 모두 간접적으로 $B$노드의 정보를 공유하고 있습니다. 즉, 두 노드 간 Causal Association이 있다고 볼 수 있습니다.
이번에는 $X$노드를 원인 변수로, $Y$노드를 결과 변수로 간주하고 살펴보겠습니다. 이 경우는 $X$ -> $W$ -> $Y$ 경로만이 간접적으로나마 Causal Association을 가집니다. 그 이외의 경로들은 인과성이 없으므로, Noncausal Association이라 할 수 있는데, 이러한 경로들을 Backdoor Path라고 하며, 아래와 같습니다.
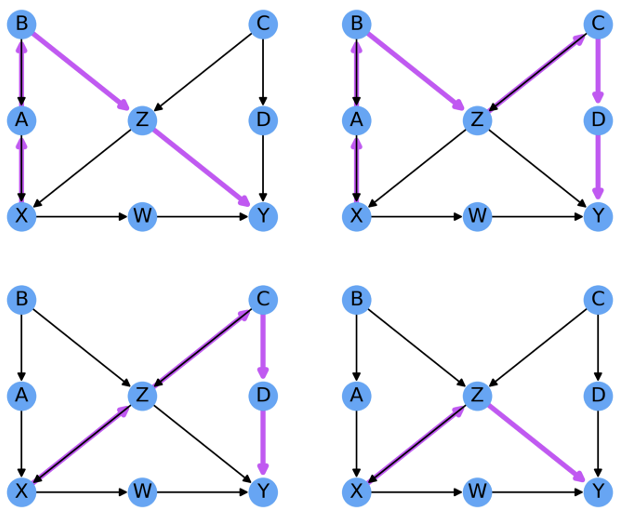
정리하자면, Structural Causal Model을 활용한 인과추론 방법은 위와 같은 Noncausal Association을 만드는 모든 Backdoor Path들을 차단함으로써 인과적인 효과를 구하는 것을 목적으로 합니다.
d-separation과 d-connection
실제로 Causal Graph는 매우 복잡합니다. 그 안에는 수많은 Mediator와 Confounder, 그리고 Collider가 복잡하게 존재할 것입니다. 복잡한 그래프 내에서 임의의 두 노드가 의존성을 가지고 있는지 혹은 분리되어 있는지를 확인할 수 있는데, 이러한 일종의 규칙을 d-separation이라고 합니다. 여기서의 d는 ‘방향성(direction)’을 의미합니다. 그림을 보면서 이해해보겠습니다.
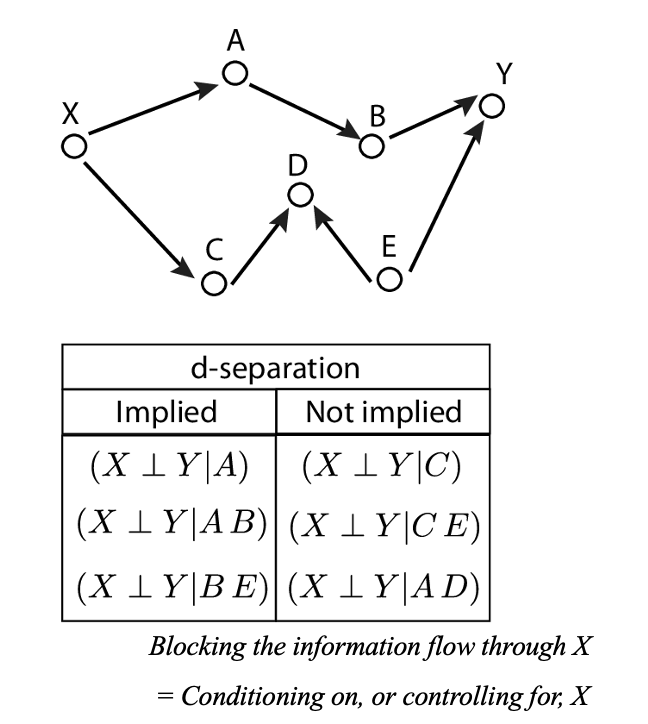
위 그래프에서 ‘특정 노드로 가는 경로를 차단하는 행위’를 Conditioning이라고 표현합니다. 원래 그래프에서는 노드 $X$에서 $Y$는 연결되어 있습니다. 즉, d-connected되어 있죠. 그런데, 만약 노드 $A$를 Conditioning 한다고 하면, $A$노드로 향하는 경로가 끊겨버립니다. 이로 인해 $X$노드에서 $Y$노드로 가는 경로는 차단되는데, 이는 $X$와 $Y$ 사이의 정보 흐름이 차단되어 인과적 연관성마저 사라지게 됩니다. 즉, d-separated 되는 것입니다. 반면, 원래 그래프에서 노드 $C$로 가는 경로를 Conditioning하여 차단한다 하더라도, $X$노드에서 $Y$노드는 연결되어 있습니다. 즉, d-connection 되어 있는 것입니다.
do-operator
Structural Causal Model은 이처럼 복잡한 그래프에서 Noncausal Association을 만드는 Backdoor Path들을 Conditioning 함으로써 인과관계 효과를 분석하는 방식입니다. 그런데 그래프가 매우 복잡한 상황에서 이러한 행위들을 일일이 손으로 한땀한땀 할 수는 없겠죠. Structural Causal Model을 개척한 Judea Pearl 교수님은 이 과정을 체계적으로 수행하고 분석하기 위해서 do-operator를 제안합니다.
do-operator는 Confounder로 인해 Backdoor Path가 열려있는 상황에서 Backdoor Path를 차단하는 방법으로, 원인 변수에 영향을 주는 모든 요인을 배제하는 상태로 만들어주는 연산입니다. 복잡합니다. 그런데, 개념만 이해하자면, 앞서 Potential Outcomes Framework에서의 Counterfactual처럼 실제로 구할 수 있는 개념이라기보다는 추상적인 개념입니다. 즉, 물리적으로 실제 그래프에서 원인 변수에 영향을 주는 요인을 차단한다기 보다는 상상속에서 이루어진다고 생각하면 좋을 것 같네요.
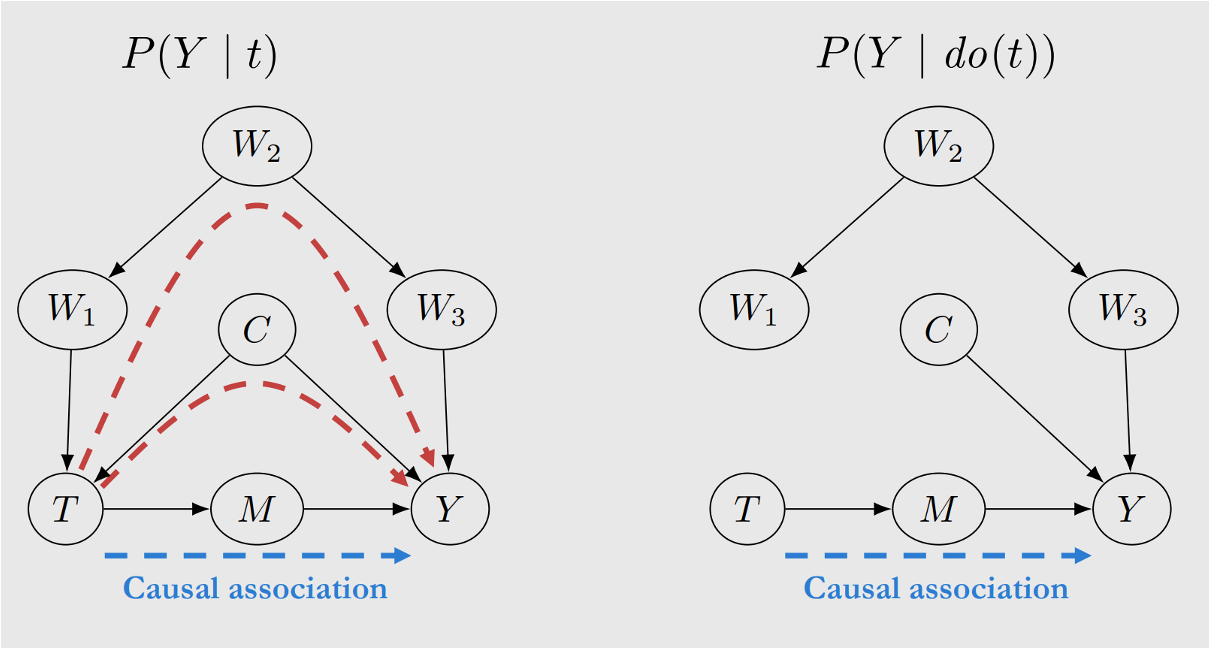
위의 그림을 살펴보며 이해해봅시다. $T$노드가 $Y$노드와 인과적 연관성이 있는지 분석하고자 하는데, 왼쪽의 방식은 빨간 점선으로 표현되는 Backdoor Path가 열려있어서 인과관계 분석이 어렵습니다. 오른쪽과 같이 do-operator를 적용하여 상상속에서 Backdoor Path를 차단한다면, $T$노드와 $Y$노드의 인과적 연관성을 쉽게(?) 구할 수 있어보입니다.
그런데 do-operator가 추상적 개념인데 이것을 도대체 어떻게 계산할 수 있다는 것일까요? do-operator로 표현한 그래프는 실제로 계산이 가능한 조건부확률의 형태로 변환하여 계산할 수 있는데, Judea Pearl 교수님은 이를 가능하도록 하는 일종의 수학적 규칙 집합인 do-calculus를 제안했습니다. 이러한 일련의 과정을 Identification이라고 합니다. 이때, Identification이 적용되어 변환이 되는 경우도 있겠으나, 불가능한 경우도 있으며, 이러한 Non-identifiable한 경우는 주어진 그래프로 인과적 효과를 구할 수 없음을 의미합니다.
정리하자면, Structural Causal Model은 어떠한 현상에 대해서 변수 간의 관계 등을 그래프 형태로 표현하는 방법을 제시하였고, do-operator를 통해서 인과적인 효과를 추론하고자 하는 접근 방법이라고 이해할 수 있겠습니다.
정리하며
이번 포스트에서는 인과추론의 양대산맥인 Potential Outcomes Framework와 Structural Causal Model을 간략하게나마 훑어보았습니다. 내용이 정말로 방대하고 어려워서 많은 공부의 필요성을 느낍니다. 본 포스트의 주 참고 자료인 인과추론의 데이터과학이 큰 도움이 된 것 같습니다. 이후에는 본 포스트에서 다룬 주요 내용들을 더욱 자세히 살펴본 후 정리하겠습니다.