(인과추론의 데이터과학) Bayesian Network의 증명

이 포스트는 개인적으로 공부한 내용을 정리하고 필요한 분들에게 지식을 공유하기 위해 작성되었습니다.
지적하실 내용이 있다면, 언제든 댓글 또는 메일로 알려주시기를 바랍니다.

본 포스트 내용은 인과추론의 데이터과학, 베이지안 네트워크 (Bayesian Network) 강의를 정리한 것임을 밝힙니다.

00. 목표

• Causal Graph 상의 $X$와 $Y$가 서로 독립인지 증명을 통해서 확인하고자 함
  • 독립이라면, $X$와 $Y$ 간 Association(i.e., Correlation)이 존재하지 않음
  • 종속이라면, $X$와 $Y$ 간 Association(i.e., Correlation)이 존재함
• 이를 위해, 두 변수 간의 관계를 $P(X,Y)=P(X)P(Y)$로 표현할 수 있는지 확인하고자 함

01. Mediator

• 원인 변수 $X$는 Mediator M에 영향을 미친 후 결과 변수 $Y$에 영향을 줌
• 이때 Mediator M을 Conditioning하여 막으면, 정보 흐름이 막히게되어 $X$와 $Y$ 간의 Correlation(Association)이 사라짐

$X$와 $Y$ 간에 Association이 있는지 증명

• $X$와 $Y$가 서로 독립이 아님을 알고싶기 때문에, (좌변)$P(X,Y) \neq$ (우변)$P(X)P(Y)$인지 확인하고자 함
• (좌변)$P(X,Y)$
  • $=\sum_{M}P(X,Y,M)$ M에 대해서 Marginalize하여 표현함
    • (참고) $P(X,Y,M) = P(X)P(M|X)P(Y|M)$ Bayesian Network Factorization
  • $=\sum_{M}P(X)P(M|X)P(Y|M)$
    
  • $=P(X)\sum_{M}P(M|X)P(Y|M)$ 정리된 좌변
    • (설명) $P(X)$는 M에 영향받지 않으므로
• (우변)$P(X)(Y)$
  • $=P(X)\sum_{M}P(Y,M)$ M에 대해서 Marginalize하여 표현함
  • $=P(X)\sum_{M}P(M)P(Y|M)$ 정리된 우변
• 만약, 정리된 좌변과 정리된 우변이 같다면, $X$와 $Y$는 독립임
  • 즉, 정리된 좌변에서의 $P(M|X)$ 부분과 정리된 우변에서의 $P(M)$부분이 같으면 독립임
  • 그러나, $P(M|X)=P(M)$이기 위해서는 $M{\bot}X$, 즉, $M$과 $X$가 독립이어야 하지만, $X \rightarrow$ M $\rightarrow Y$의 Causal Graph에서 Causal Markov Assumption에 의해 두 변수는 종속적임
• 따라서, $P(M|X) \neq P(M)$이므로, $X$와 $Y$는 종속이며, Association이 존재함

$M$을 Conditioning하면, $X$와 $Y$ 간에 Association이 사라짐을 증명

• M을 Conditioning 한다고 해도 $X$와 $Y$ 간에 Association이 있는지를 알고싶기 때문에, (좌변)$P(X,Y|M) \neq$ (우변)$P(X|M)P(Y|M)$인지 확인해야 함
• (좌변)$P(X,Y|M)$의 꼴을 만들어주기 위해서
  • $P(X,Y,M)$
  • $=P(M)P(X,Y|M)$ 정리된 좌변
• (우변)$P(X|M)P(Y|M)$의 꼴을 만들어주기 위해서
  • $P(X,Y,M)$
  • $=P(X)P(M|X)P(Y|M)$ Bayesian Network Factorization
  • $=P(M)P(X|M)P(Y|M)$ 정리된 우변
• 정리된 좌변과 정리된 우변을 이용하여
  • $P(M)P(X,Y|M)=P(M)P(X|M)P(Y|M)$
  • $P(X,Y|M)=\cfrac{P(M)P(X|M)P(Y|M)}{P(M)}=P(X|M)P(Y|M)$
• 따라서, $P(X,Y|M)=P(X|M)P(Y|M)$이 성립하므로, M을 Conditioning하면 $X$와 $Y$는 독립이되며, 두 변수 간 Association은 존재하지 않음

02. Confounder

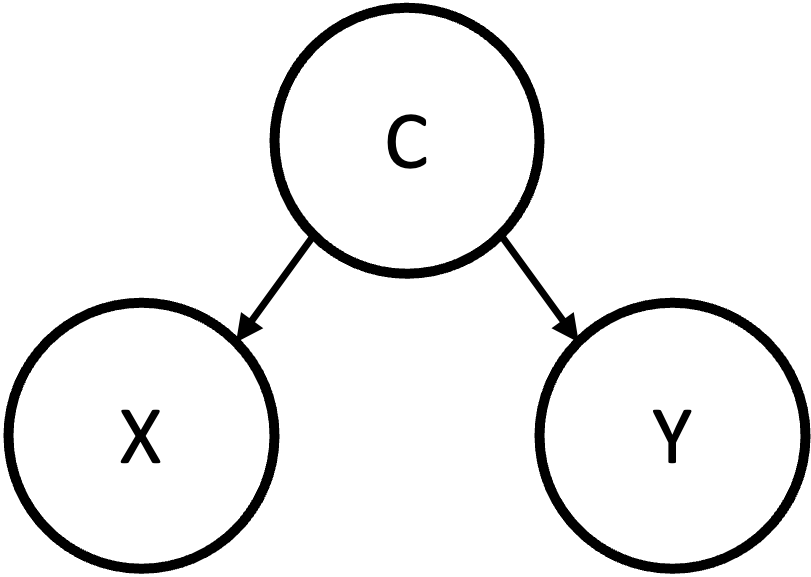
• Confounder는 $X$와 $Y$의 공통 원인이 되는 C가 존재하는 구조이며, 이는 선택 편향의 원인이 됨
• $P(X,Y,C)=P(X|C)P(Y|C)P(C)$ Bayesian Network Factorization
  • (설명) $X$와 $Y$는 부모노드 C에 영향을 받으므로 각각 $P(X|C)$, $P(Y|C)$로 표현하며, C는 어떠한 노드에도 영향받지 않으므로 $P(C)$로 표현함

$X$와 $Y$ 간에 Association이 있는지 증명

• $X$와 $Y$가 서로 독립이 아님을 알고싶기 때문에, (좌변)$P(X,Y) \neq$ (우변)$P(X)P(Y)$인지 확인하고자 함
• (좌변)$P(X,Y)$의 꼴을 이용하여
  • $P(X,Y)$
  • $= \sum_{C}P(X,Y,C)$ C에 대해서 Marginalize하여 표현함
  • $=\sum_{C}P(X|C)P(Y|C)P(C)$ Bayesian Network Factorization
  • $=\sum_{C}P(X|C)P(Y)P(C|Y)$
    • (설명) $P(Y,C) = P(Y)(C|Y) = P(Y|C)P(C)$ 이므로
  • $=P(Y) \sum_{C} P(X|C)P(C|Y)$ 정리된 좌변
    • (설명) $P(Y)$는 C에 영향받지 않으므로
• (우변)$P(X)P(Y)$의 꼴을 이용하여
  • $P(X)P(Y) = P(Y)P(X)$
  • $= P(Y) \sum_{C}P(X,C)$ C에 대해서 Marginalize하여 표현함
    • (설명) $P(X)=\sum_{C}P(X,C)$ 이므로
  • $= P(Y) \sum_{C}P(C)P(X|C)$ 정리된 우변
• 정리된 좌변과 정리된 우변을 이용하여
  • 정리된 좌변$P(Y) \sum_{C} P(X|C)P(C|Y)$와 정리된 우변$P(Y) \sum_{C}P(C)P(X|C)$를 비교하여, $P(C|Y)=P(C)$가 성립한다면, 정리된 좌변$=$정리된 우변이 성립되어, $P(X,Y)=P(X)P(Y)$가 만족됨
  • 그러나, Confounder는 $Y$ 자체가 부모노드 C에 직접적으로 영향을 받기 때문에 상호 의존 관계가 있을 수밖에 없으므로 $P(C|Y)=P(C)$가 성립될 수 없음
• 따라서, $P(C|Y) \neq P(C)$이므로, $P(X,Y) \neq P(X)(Y)$가 성립되어 $X$와 $Y$는 서로 독립일 수 없으며, C가 Conditioning되지 않는다면, 두 변수 간에는 Association이 존재함

$C$를 Conditioning하면, $X$와 $Y$ 간에 Association이 사라짐을 증명

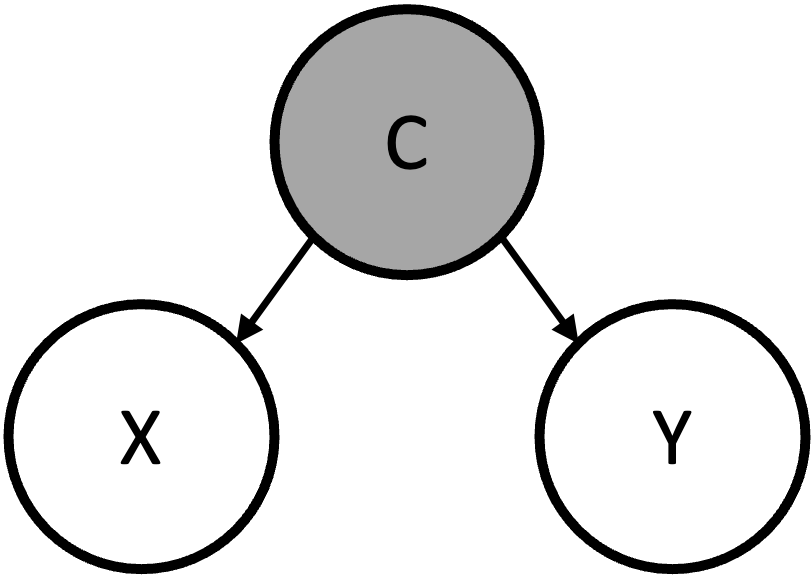
• C를 Conditioning 한다고 해도 $X$와 $Y$ 간에 Association이 있는지를 알고싶기 때문에, (좌변)$P(X,Y|C) \neq$ (우변)$P(X|C)P(Y|C)$인지 확인해야 함
• (좌변)$P(X,Y|C)$의 꼴을 만들어주기 위해서
  • $P(X,Y,C)$
  • $=P(C)P(X,Y|C)$ 정리된 좌변
• (우변)$P(X|C)P(Y|C)$의 꼴을 만들어주기 위해서
  • $P(X,Y,C)$
  • $=P(X|C)P(Y|C)P(C)$ Bayesian Network Factorization 정리된 우변
• 정리된 좌변과 정리된 우변을 이용하여
  • $P(C)P(X,Y|C)=P(X|C)P(Y|C)P(C)$
  • $P(X,Y|C)=P(X|C)P(Y|C)$가 성립됨
• 따라서, C를 Conditioning하면 $P(X,Y|C)=P(X|C)P(Y|C)$가 성립되어 $X$와 $Y$는 독립이되므로, 두 변수 간 Association이 사라짐

03. Collider

• Collider는 $X$와 $Y$가 원인이되어 공통의 결과인 C를 만들어내는 구조임
• Collider는 C를 Conditioning하지 않으면 $X$와 $Y$ 간에 Association이 존재하지 않음
• 그런데, C를 Conditioning하면, $X$와 $Y$ 간에 Association이 형성됨
• $P(X,Y,C)=P(X)P(Y)P(C|X,Y)$ Bayesian Network Factorization
  • (설명) $X$와 $Y$는 자신에게 직접적인 영향을 주는 부모노드가 없으므로, 각각 $P(X)$, $P(Y)$로 표현하며, C는 $X$와 $Y$에 직접적인 영향을 받으므로 $P(C|X,Y)$로 표현함

$X$와 $Y$ 간에 Association이 있는지 증명

• $X$와 $Y$가 서로 독립이 아님을 알고싶기 때문에, (좌변)$P(X,Y) \neq$ (우변)$P(X)P(Y)$인지 확인하고자 함
• (좌변)$P(X,Y)$ 정리된 좌변
• (우변)$P(X)P(Y)$의 꼴을 이용하기 위해서
  • $P(X,Y) = \sum_{C}P(X,Y,C)$ C에 대해서 Marginalize하여 표현함
  • $\sum_{C}P(X)P(Y)P(C|X,Y)$
    • (설명) Collider 구조에서의 Bayesian Network Factorization에 의하여
  • $=P(X)P(Y)\sum_{C}P(C|X,Y)$
    • (설명) Marginal Probability $P(X)$와 $P(Y)$는 C에 영향받지 않으므로
  • $=P(X)P(Y)$ 정리된 우변
    • (설명) 결과 C를 도출할 수 있는 모든 확률값의 합은 항상 $\sum_{C}P(C|X,Y)=1$이 성립하므로
• 정리된 좌변과 정리된 우변을 이용하여
  • $P(X,Y)=P(X)P(Y)$가 성립됨
• 따라서, C가 Conditioning되지 않는다면, $P(X,Y)=P(X)P(Y)$가 성립되어 두 변수는 독립이 되며, Association이 존재하지 않음

$C$를 Conditioning하면, $X$와 $Y$ 간에 Association이 생겨남을 증명

• C를 Conditioning 할 때 $X$와 $Y$ 간에 Association이 있는지를 알고싶기 때문에, (좌변)$P(X,Y|C)=$ (우변)$P(X|C)P(Y|C)$인지 확인해야 함
• 그러나, Collider의 경우, 위의 식이 아닌, (좌변)$P(X|C)=$(우변)$P(X|C,Y)$가 성립하는지를 대신하여 검토함으로써 독립 여부를 확인할 수 있음
  • (설명) (좌변)과 달리, (우변)에서는 $Y$까지 Conditioning 하였는데, 위를 만족할 경우, $C$가 Conditioning 되어있다면 이미 독립이 성립하여, $Y$가 추가로 Conditioning 되는지 여부가 아무런 영향을 주지 않는다고 해석할 수 있음
• (좌변)$P(X|C)$을 이용하여
  • $P(X|C)$
  • $=\cfrac{P(X)P(C|X)}{P(C)}$ 정리된 좌변
• (우변)$P(X|C,Y)$의 꼴을 만들어주기 위해서 다음과 같은 트릭을 사용함
  • $P(X,C|Y)$ 일종의 트릭?으로 시작함
    • $=P(X|Y)P(C|Y,X)$ 도출된 식 1
    • $=P(C|Y)P(X|Y,C)$ 도출된 식 2
    • 도출된 식 1과 도출된 식 2를 이용하여
      • $P(X|Y)P(C|Y,X) = P(C|Y)P(X|Y,C)$
      • $\cfrac{P(X|Y)P(C|Y,X)}{P(C|Y)} = P(X|Y,C) = P(X|C,Y)$ 정리된 우변
• 정리된 좌변과 정리된 우변을 이용하여
  • $\cfrac{P(X)P(C|X)}{P(C)} = \cfrac{P(X|Y)P(C|Y,X)}{P(C|Y)}$이라면 $X$와 $Y$는 독립이 성립함
  • 이를 정리하면, $\cfrac{P(C|X)}{P(C)} = \cfrac{P(C|Y,X)}{P(C|Y)}$로 표현할 수 있음
    • (설명) Collider에서는 $Y$를 Conditioning 하는지 여부와 상관없이 독립이므로, $P(X)=P(X|Y)$가 성립함
• 따라서, $\cfrac{P(C|X)}{P(C)} = \cfrac{P(C|Y,X)}{P(C|Y)}$가 성립하는지를 확인하면 됨
  • 좌변식은 $X$를 Conditioning하지 않았을 때에 대비하여, $X$를 Conditioning 했을 때 $C$에 미치는 영향(Effect of $X$ on $C$)을 의미함
  • 우변식은 $Y$가 Conditioning 되어있는 상황에서 $X$를 Conditioning하지 않았을 때에 대비하여, $Y$가 Conditioning 되어있는 상황에서 $X$를 Conditioning 했을 때 $C$에 미치는 영향(Effect of $X$ on $C$ after controlling for Y)을 의미함
  • 그러나, Multivariate Regression에서도 그러하듯, 어떠한 통제 변수가 추가되면 나머지 요인들도 반드시 영향을 받게됨
    • 더욱 수학적인 증명은 생략함
• 따라서, 추가된 통제 변수 $Y$는 반드시 결과에 영향을 미치기 때문에 $\cfrac{P(C|X)}{P(C)} \neq \cfrac{P(C|Y,X)}{P(C|Y)}$이 됨
• 따라서, Collider에서는 C를 Conditioning하면 $X$와 $Y$의 관계가 독립이 아니게되어 두 변수 간 Association이 생겨남