(인과추론의 데이터과학) Bayesian Network의 개념

이 포스트는 개인적으로 공부한 내용을 정리하고 필요한 분들에게 지식을 공유하기 위해 작성되었습니다.
지적하실 내용이 있다면, 언제든 댓글 또는 메일로 알려주시기를 바랍니다.

본 포스트 내용은 인과추론의 데이터과학, 베이지안 네트워크 (Bayesian Network) 강의를 정리한 것임을 밝힙니다.

• Probability
  • $P(A)$
    • A라는 사건이 일어날 확률, 다른 사건에 전혀 영향받지 않음
    • Unconditional Probability 또는 Marginal Probability라고도 불림
  • $P(A|B)$
    • B라는 사건이 일어난 상황에서 A라는 사건이 일어날 조건부 확률
    • Conditional Probability라고 불림
  • $P(A{\cap}B)=P(A,B)$
    • A라는 사건과 B라는 사건이 동시에 나타날 확률
    • Joint Probability라고 불림
    • 1) $=P(A)P(B|A)$
      • A가 일어났고, A가 일어난 상황에서 B가 일어난 확률
    • 2) $=P(B)P(A|B)$
      • B가 일어났고, B가 일어난 상황에서 A가 일어난 확률
    • a와 b를 이용하여 Bayes' Theorem을 정의할 수 있음
      • $P(B|A) = \cfrac{P(B)P(A|B)}{P(A)}$
• Joint Probability
  • $P(A,B,C) = P(A)P(B,C|A) = P(A)P(B|A)P(C|A,B)$
  • Joint Probability는 바로 계산할 수 없으므로, Chain Rule을 통해 Conditional Probability로 풀어준 후 계산함
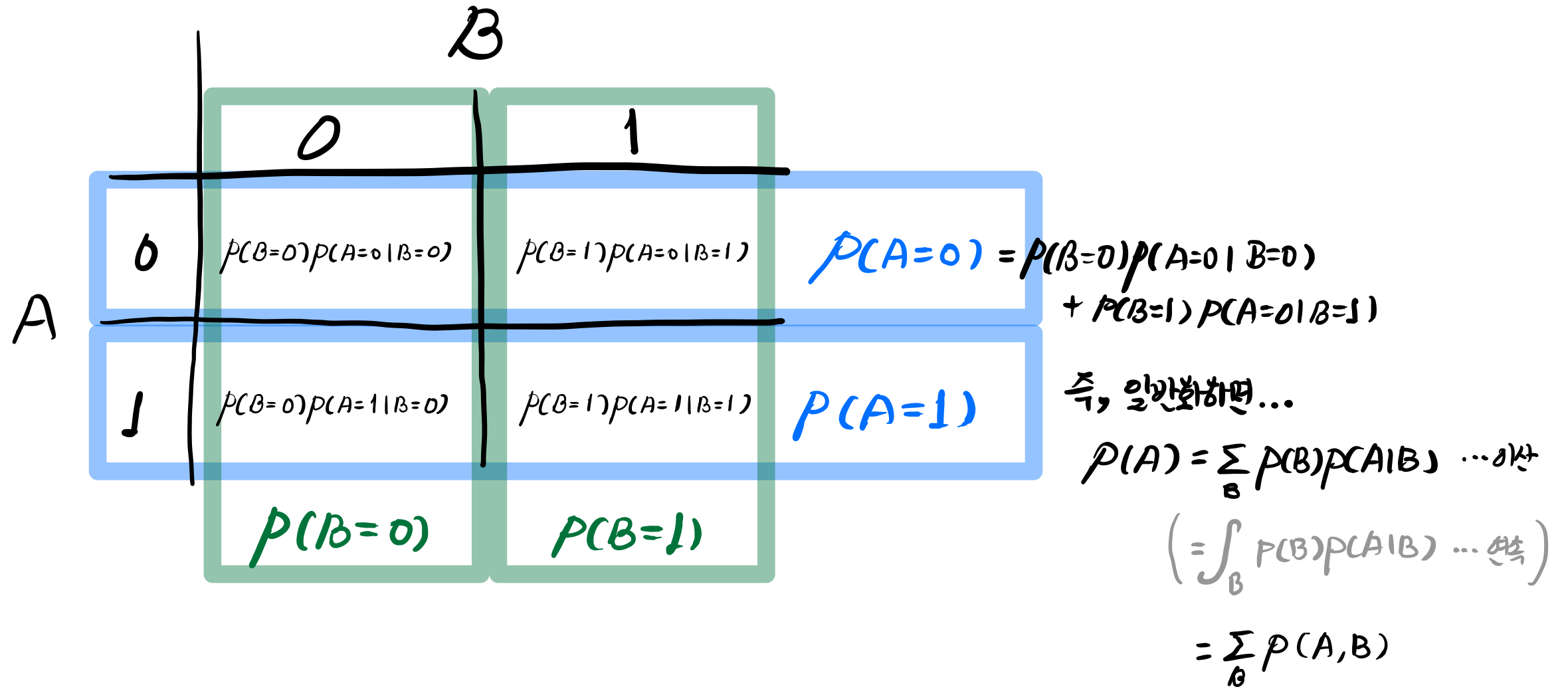
• Marginalize
  • Conditional Probability 또는 Joint Probability를 Marginal Probability로 바꾸는 작업
  • (예)
• Independent
  • $A{\bot}B$
    • Orthogonal 함
  • $P(A|B)=P(A)$
  • $P(A,B)=P(A)P(B|A)=P(A)P(B)$
  • $\Leftrightarrow$ Dependent (Correlation 또는 Association이 있음)
• Conditional Independent
  • 특정 조건 하에서(Conditioning 했을 때) 독립이 되는 경우임
  • $(A,B|C)=P(A|C)P(B|C)$
    • $C$라는 조건 하에서 $A$와 $B$가 독립이 됨
• Causal Markov Assumption (under DAG)
  • Directly Acyclic Graph(DAG)가 주어져야지만 Causal Markov Assumption을 가정할 수 있음
  • 만약, 그래프가 없는 상황에서 Joint Probability를 계산한다면, Chain Rule을 적용해서 풀어야 함
    • (e.g.) $P(X,Y,Z)=P(X)P(Y,Z|X)=P(X)P(Y|X)P(Z|X,Y)$
  • Causal Markov Assumption은 그래프에서 자신에게 직접적인 영향을 주는 노드에만 영향을 받는다는 가정임
    • (e.g.) 그래프가 $X \rightarrow Y \rightarrow Z$로 주어졌고, 여기에 Causal Markov Assumption을 적용한다면?
      • $P(X,Y,Z)=P(X)P(Y|X)P(Z|Y)$
      • 즉, $P(Z|Y)$를 보면, $Z$는 자신에게 직접적인 영향을 주는 부모 노드인 $Y$만을 조건으로 함
  • 이처럼 Causal Graph의 Joint Probability를 조건부 확률꼴로 분해하는 것을 Bayesian Network Factorization이라고 함